题目内容
19.解不等式(组)①5x<2x-3
②$\left\{\begin{array}{l}{2(x+1)>4}\\{3x≤x+5}\end{array}\right.$.
分析 (1)不等式移项合并,将x系数化为1,求出解集.
(2)先求出各不等式的解集,再求其公共解集即可.
解答 解:(1)移项得:5x-2x<-3,
合并同类项得:3x<-3,
∴x<-1;
(2)$\left\{\begin{array}{l}{2(x+1)>4①}\\{3x≤x+5②}\end{array}\right.$
由不等式①式得:x>1,
由不等式②式得:x$≤\frac{5}{2}$;
∴此不等式组的解为:1<x≤$\frac{5}{2}$.
点评 此题主要考查了一元一次不等式(组)的解法,关键是掌握求不等式组解集的口诀:同大取大,同小取小,大小小大中间找,大大小小找不到(无解).

练习册系列答案
相关题目
10.下列图形是中心对称图形但不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
14.若a>b,则下列结论正确的是( )
| A. | a-5<b-5 | B. | a+2<b+2 | C. | 3a<3b | D. | -3a<-3b |
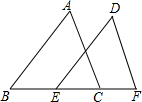 如图,已知:∠B=∠DEF,BC=EF,现要证明△ABC≌△DEF,若要以“SAS”为依据,还缺条件AB=DE;若要以“ASA”为依据,还缺条件∠ACB=∠DFE,若要以“AAS”为依据,还缺条件∠A=∠D.
如图,已知:∠B=∠DEF,BC=EF,现要证明△ABC≌△DEF,若要以“SAS”为依据,还缺条件AB=DE;若要以“ASA”为依据,还缺条件∠ACB=∠DFE,若要以“AAS”为依据,还缺条件∠A=∠D.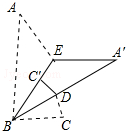 如图,△ABC中,∠A=35°,沿BE将此三角形对折,又沿BA′再一次对折,点C落在BE上的C′处,此时∠C′DB=85°,则原三角形的∠ABC的度数为( )
如图,△ABC中,∠A=35°,沿BE将此三角形对折,又沿BA′再一次对折,点C落在BE上的C′处,此时∠C′DB=85°,则原三角形的∠ABC的度数为( )