题目内容
10、如图，∵BE平分∠ABC（已知）∴
∠ABC
=2∠1（角平分线的定义）∵CE平分∠DCB（已知）
∴
∠DCB
=2∠2（角平分线的定义）∴
∠ABC
+∠DCB
=2∠1+2∠2=2（∠1+∠2）又∵∠1+∠2=90°（已知）
∴
∠ABC
+∠DCB
=2×90°=180°，∴
AB
∥CD
（同旁内角互补，两直线平行
）．分析：根据角平分线的定义及同旁内角互补，两直线平行的判定定理便可解答．
解答：解：∵BE平分∠AB（已知）
∴∠ABC=2∠1（角平分线的定义）
∵CE平分∠DCB（已知）
∴∠DCB=2∠2（角平分线的定义）
∴∠ABC+∠DCB=2∠1+2∠2=2（∠1+∠2）
又∵∠1+∠2=90°（已知）
∴∠ABC+∠DCB=2×90°=180°
∴AB∥CD（同旁内角互补，两直线平行）．
∴∠ABC=2∠1（角平分线的定义）
∵CE平分∠DCB（已知）
∴∠DCB=2∠2（角平分线的定义）
∴∠ABC+∠DCB=2∠1+2∠2=2（∠1+∠2）
又∵∠1+∠2=90°（已知）
∴∠ABC+∠DCB=2×90°=180°
∴AB∥CD（同旁内角互补，两直线平行）．
点评：本题是考查平行线的判定的基础题，比较容易，稍作转化即可．
练习册系列答案
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
名师指导一卷通系列答案
相关题目
14、如图，BE平分∠ABC，DE∥BC，∠EBC=25°，则∠ADE=
如图，BE平分∠ABD，DE平分∠BDC，且BE⊥DE于E，那么AB∥CD吗？（ ）
完成下面的证明：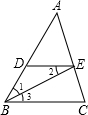
已知：如图，BE平分∠ABC，∠1=∠2．那么BC与DE平行吗？请说明理由．
已知，如图，BE平分∠ABC，DE∥BC，∠3=35°，求∠1的度数