题目内容
15.已知x2+2x-8=0,求代数式$\frac{1}{{{x^2}-1}}÷\frac{x+1}{{{x^2}-2x+1}}-\frac{1}{x+1}$的值.分析 首先将原式分母分解因式进而利用分式除法运算法则化简,进而求出即可.
解答 解:原式=$\frac{1}{(x+1)(x-1)}$×$\frac{(x-1)^{2}}{x+1}$-$\frac{1}{x+1}$,
=$\frac{x-1}{(x+1)^{2}}$-$\frac{1}{x+1}$,
=$\frac{x-1}{(x+1)^{2}}$-$\frac{x+1}{(x+1)^{2}}$,
=-$\frac{2}{(x+1)^{2}}$,
=-$\frac{2}{{x}^{2}+2x+1}$,
∵x2+2x-8=0,
∴x2+2x=8,
∴原式=-$\frac{2}{9}$.
点评 此题主要考查了分式的化简求值,正确分解因式是解题关键.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
3. 如图,数轴上有A,B,C,D四个点,其中表示2的相反数的点是( )
如图,数轴上有A,B,C,D四个点,其中表示2的相反数的点是( )
 如图,数轴上有A,B,C,D四个点,其中表示2的相反数的点是( )
如图,数轴上有A,B,C,D四个点,其中表示2的相反数的点是( )| A. | 点A | B. | 点B | C. | 点C | D. | 点D |
7.若把代数式x2-2x+3化为(x-m)2+k形式,其中m,k为常数,结果为( )
| A. | (x+1)2+4 | B. | (x-1)2+2 | C. | (x-1)2+4 | D. | (x+1)2+2 |
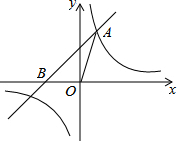 如图,已知在直角坐标系xOy中,O是坐标原点,点A(2,5)在反比例函数y=$\frac{k}{x}$的图象上,过点A的一次函数y=x+b的图象交x轴于点B.
如图,已知在直角坐标系xOy中,O是坐标原点,点A(2,5)在反比例函数y=$\frac{k}{x}$的图象上,过点A的一次函数y=x+b的图象交x轴于点B.
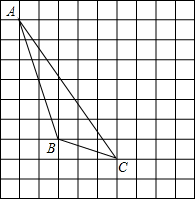 如图,每个小正方形的边长为1个单位.
如图,每个小正方形的边长为1个单位. 如图,⊙O的半径为6,AO⊥BC,∠D=30°,则弦BC的长为6$\sqrt{3}$.
如图,⊙O的半径为6,AO⊥BC,∠D=30°,则弦BC的长为6$\sqrt{3}$.