题目内容
16.有一列数x1,x2,x3,…,x4中,已知x1=1,且当k≥2时,xk=xk-1+1-4([$\frac{k-1}{4}$]-[$\frac{k-2}{4}$])(取整符号[a]表示不超过实数a的最大整数,如[2,6]=2,[0,2]=0),则x2016等于4.分析 根据当k≥2时,xk=xk-1+1-4([$\frac{k-1}{4}$]-[$\frac{k-2}{4}$]),找出部分xn的值,根据数的变化即可得出“x4n+1=1,x4n+2=2,x4n+3=3,x4n+4=4(n为自然数)”由此即可得出结论.
解答 解:∵当k≥2时,xk=xk-1+1-4([$\frac{k-1}{4}$]-[$\frac{k-2}{4}$]),
∴x2=2,x3=3,x4=4,x5=1,x6=2,x7=3,x8=4,x9=1,…,
∴x4n+1=1,x4n+2=2,x4n+3=3,x4n+4=4(n为自然数).
∵2016=504×4,
∴x2016=4.
故答案为:4.
点评 本题考查了规律型中数字的变化类,解题的关键是根据数与数之间的关系找出数的变化规律x4n+1=1,x4n+2=2,x4n+3=3,x4n+4=4(n为自然数)是关键.

练习册系列答案
相关题目
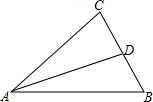 如图所示,已知AD是△ABC的中线.
如图所示,已知AD是△ABC的中线.