Question

给定直线l：y=kx，抛物线C：y=ax²+bx+1．

（1）当b=1时，l与C相交于A，B两点，其中A为C的顶点，B与A关于原点对称，求a的值；

（2）若把直线l向上平移k²+1个单位长度得到直线r，则无论非零实数k取何值，直线r与抛物线C都只有一个交点．

①求此抛物线的解析式；

②若P是此抛物线上任一点，过P作PQ∥y轴且与直线y=2交于Q点，O为原点．求证：OP=PQ．

Answer 1

（1）解：

∵l：y=kx，C：y=ax²+bx+1，当b=1时有A，B两交点，

∴A，B两点的横坐标满足kx=ax²+x+1，即ax²+（1﹣k）x+1=0．

∵B与A关于原点对称，

∴0=x_A+x_B=，

∴k=1．

∵y=ax²+x+1=a（x+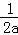）²+1﹣，

∴顶点（﹣，1﹣）在y=x上，

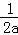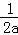∴﹣=1﹣，

解得 a=﹣．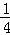

（2）

①解：∵无论非零实数k取何值，直线r与抛物线C都只有一个交点，

∴k=1时，k=2时，直线r与抛物线C都只有一个交点．

当k=1时，r：y=x+2，

∴代入C：y=ax²+bx+1中，有ax²+（b﹣1）x﹣1=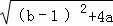0，

∵△==0，

∴（b﹣1）²+4a=0，

当k=2时，r：y=2x+5，

∴代入C：y=ax²+bx+1中，有ax²+（b﹣2）x﹣4=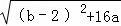0，

∵△==0，

∴（b﹣2）²+16a=0，

∴联立得关于a，b的方程组 ，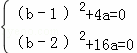

解得 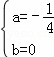或 ．

∵r：y=kx+k²+1代入C：y=ax²+bx+1，得ax²+（b﹣k）x﹣k²=0，

∴△=．

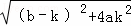当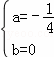时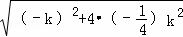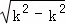，△===0，故无论k取何值，直线r与抛物线C都只有一个交点．

当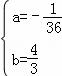时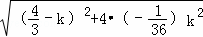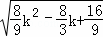，△==，显然虽k值的变化，△不恒为0，所以不合题意舍去．

∴C：y=﹣x²+1．

②证明：

根据题意，画出图象如图1，

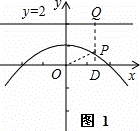
由P在抛物线y=﹣x²+1上，设P坐标为（x，﹣x²+1），连接OP，过P作PQ⊥直线y=2于Q，作PD⊥x轴于D，

∵PD=|﹣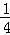x²+1|，OD=|x|，

∴OP====，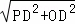

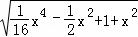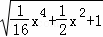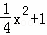  PQ=2﹣y_P=2﹣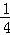（﹣x²+1）=，

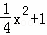∴OP=PQ．