题目内容
19．已知a4+b4+2a2b2-2a2-2b2-15=0．求代数式a2+b2的值．分析 利用因式分解把原式变为（a2+b2+3）（a2+b2-5）=0，结合非负数的性质得出答案即可．
解答 解：∵a4+b4+2a2b2-2a2-2b2-15=0，
∴（a2+b2）2-2（a2+b2）-15=0，
∴（a2+b2+3）（a2+b2-5）=0，
∴a2+b2=-3，a2+b2=5，
∵a2+b2≥0，
∴a2+b2=5．
点评 此题考查因式分解的实际运用，非负数的性质，把a2+b2看作一个整体因式分解是解决问题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
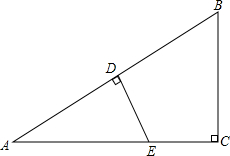如图，在Rt△ABC中，AC=10，BC=6，∠C=90°，D为AB中点，DE⊥AB于D交AC于E，求CE长．
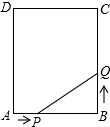如图．矩形ABCD中，AB=6cm，BC=10cm，点P从A开始沿AB边向点B以1厘米/秒的速度移动，点Q从点B开始沿BC边向点C以2厘米/秒的速度移动，如果P、Q分别是从A、B同时出发，经过几秒，五边形APQCD的面积等于52平方厘米？
4．某化肥厂生产的化肥产量经过两年增长21%，则每年比上一年平均增长的百分数为（ ）
| A． | 10% | B． | 10.5% | C． | 11% | D． | 12% |