题目内容
9.某工厂用如图甲所示的长方形和正方形纸板,做成如图乙所示的竖式与横式两种长方体形状的无盖纸盒.(1)现有正方形纸板162张,长方形纸板340张.若要做两种纸盒共l00个,有哪几种生产方案?
(2)若有正方形纸板162张,长方形纸板a张,做成上述两种纸盒,纸板恰好用完.已知290<a<306.求a的值.
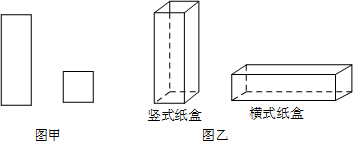
分析 (1)设生产竖式纸盒x个,则生产横式纸盒(100-x)个.根据生产竖式纸盒用的正方形纸板+生产横式纸盒用的正方形纸板≤162张;生产竖式纸盒用的长方形纸板+生产横式纸盒用的长方形纸板≤340张.由此,可得出不等式组,求出自变量的取值范围,然后得出符合条件的方案.
(2)设x个竖式需要正方形纸板x张,长方形纸板横4x张;y个横式需要正方形纸板2y张,长方形纸板横3y张,可列出方程组,再根据a的取值范围求出y的取值范围即可.
解答 解:(1)设生产竖式纸盒x个,则生产横式纸盒(100-x)个.由题意得
$\left\{\begin{array}{l}{x+2(100-x)≤162}\\{4x+3(100-x)≤340}\end{array}\right.$,
解得38≤x≤40.
答:共有三种生产方案,方案一:生产竖式纸盒38个,横式纸盒62个;
方案二:生产竖式纸盒39个,横式纸盒61个;
方案三:生产竖式纸盒40个,横式纸盒60个.
(2)设生产竖式纸盒x个,则生产横式纸盒y个.由题意得
$\left\{\begin{array}{l}{x+2y=162}\\{4x+3y=a}\end{array}\right.$ 解得y=$\frac{648-a}{5}$
∵290<a<306,
∴342<648-a<358
∵y是整数,
∴648-a=345,350,355.
此时$\left\{\begin{array}{l}{a=293}\\{x=20}\\{y=71}\end{array}\right.$;$\left\{\begin{array}{l}{a=298}\\{x=22}\\{y=70}\end{array}\right.$;$\left\{\begin{array}{l}{a=303}\\{x=24}\\{y=69}\end{array}\right.$
∴a=303,298,293.
点评 本题考查一元一次不等式组的应用,将现实生活中的事件与数学思想联系起来,读懂题列出不等式关系式即可求解.

 阅读快车系列答案
阅读快车系列答案| 甲种品牌化妆品 | 球 | 两红 | 一红一白 | 两白 |
| 礼金券(元) | 6 | 12 | 6 |
| 乙种品牌化妆品 | 球 | 两红 | 一红一白 | 两白 |
| 礼金券(元) | 12 | 6 | 12 |
(2)如果一个顾客当天在本店购物满88元,若只考虑获得最多的礼品券,请你帮助分析选择购买哪种品牌的化妆品?并说明理由.
| A. | 了解武汉市民消费水平 | B. | 了解全班同学每周体育锻炼的时间 | ||
| C. | 了解武汉市中学生的眼睛视力情况 | D. | 了解一批节能灯的使用寿命情况 |
| A. | 有限小数不是有理数 | B. | 无限小数是无理数 | ||
| C. | 数轴上的点与有理数一一对应 | D. | 数轴上的点与实数一一对应 |
 如图,直线a,b都与直线c相交,给出的下列条件:
如图,直线a,b都与直线c相交,给出的下列条件: