题目内容
已知M=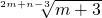
是m+3的算术平方根，N=
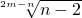是n-2的立方根．求（n-m）2008．
解：∵M=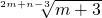是m+3的算术平方根，N=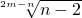是n-2的立方根
∴2m+n-3=2，2m-n=3
∴m=2，n=1
∴（n-m）2008=1．
分析：由于算术平方根的根指数为2，立方根的根指数为3，由此可以列出关于m、n的方程组，解方程组求出m和n，进而代入所求代数式求解即可．
点评：此题主要考查了算术平方根、立方根的定义．解决本题的关键是利用根的指数知识得到未知字母的值．
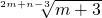是m+3的算术平方根，N=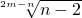是n-2的立方根∴2m+n-3=2，2m-n=3
∴m=2，n=1
∴（n-m）2008=1．
分析：由于算术平方根的根指数为2，立方根的根指数为3，由此可以列出关于m、n的方程组，解方程组求出m和n，进而代入所求代数式求解即可．
点评：此题主要考查了算术平方根、立方根的定义．解决本题的关键是利用根的指数知识得到未知字母的值．
练习册系列答案
相关题目
如图，已知O是?ABCD的对角线的交点，AC=6，BD=8，AB=5，请你算出四边形ABCD的周长．
小红家有一块L形菜地，要把L形菜地按如图所示的那样分成面积相等的两个梯形种上不同的蔬菜．已知这两个梯形的上底都是a米，下底都是b米，高都是（b-a）米．
，
）的抛物线交
轴于
点，交
轴于
，
两点（点
，
）。
的垂线交抛物线于点
，如果以点
相切，请判断抛物线的对称轴
与⊙
是抛物线上的一个动点，且位于
交于点
问：当点
的长度最大？并求出此时△
的面积。
，知道
，可求出PQ 的长度，从而求出最大值和P点坐标，再根据三角形的面积公式求出面积
，
）的抛物线交
轴于
点，交
轴于
，
两点（点
，
）。
的垂线交抛物线于点
，
如果以点
相切，请判断抛物线的对称轴
与⊙
是抛物线上的一个动点，且位于
交于点
问：当点
的长度最大？并求出此时△
的面积。
，知道
，可求出PQ 的长度，从而求出最大值和P点坐标，再根据三角形的面积公式求出面积