题目内容
6.抛物线C:y=x2-4x+b的顶点E在直线y=$\frac{1}{2}$x-3上,求抛物线C关于直线y=-1轴对称的抛物线的解析式.分析 把抛物线解析式整理成顶点式形式,然后写出顶点坐标,再代入直线解析式计算即可求出b的值,然后求得抛物线C关于直线y=-1轴对称的抛物线的顶点坐标,由此可以求得新抛物线的解析式.
解答 解:由y=x2-4x+b=(x-2)2+b-4得到:E(2,b-4),
将其代入直线y=$\frac{1}{2}$x-3,得b-4=$\frac{1}{2}$×2-3,
解得b=2.
则顶点(2,-2)关于直线y=-1轴对称的坐标为(2,0),
设抛物线C关于直线y=-1对称的抛物线解析式为y=a(x-2)2过点(0,-4),
则-4=a(0-2)2,
解得a=-1.
所以该抛物线的解析式为:y=-(x-2)2.
点评 本题考查了二次函数图象与几何变换.求出变换后抛物线的顶点坐标是解题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
17. 如图,四边形ABCD中,AB=AC=AD,∠CBD=23°,则∠CAD为( )
如图,四边形ABCD中,AB=AC=AD,∠CBD=23°,则∠CAD为( )
 如图,四边形ABCD中,AB=AC=AD,∠CBD=23°,则∠CAD为( )
如图,四边形ABCD中,AB=AC=AD,∠CBD=23°,则∠CAD为( )| A. | 47° | B. | 46° | C. | 45° | D. | 44° |
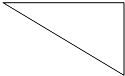 小芳想在墙壁上钉一个三角架(如图),其中两直角边长度之比为3:2,斜边长$\sqrt{520}$厘米,求两直角边的长度.
小芳想在墙壁上钉一个三角架(如图),其中两直角边长度之比为3:2,斜边长$\sqrt{520}$厘米,求两直角边的长度.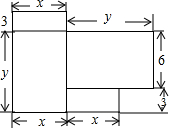 小明家最近刚购置了一套商品房,如图是这套商品房的平面图(单位:m).
小明家最近刚购置了一套商品房,如图是这套商品房的平面图(单位:m). 如图,已知四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF.
如图,已知四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF.