题目内容
12.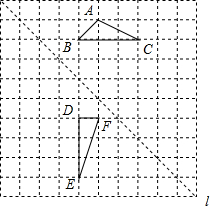 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC和△DEF(顶点为网格线的交点),以及过格点的直线l.
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC和△DEF(顶点为网格线的交点),以及过格点的直线l.(1)将△ABC向右平移两个单位长度,再向下平移两个单位长度,画出平移后的三角形.
(2)画出△DEF关于直线l对称的三角形.
(3)填空:∠C+∠E=45°.
分析 (1)将点A、B、C分别右移2个单位、下移2个单位得到其对应点,顺次连接即可得;
(2)分别作出点D、E、F关于直线l的对称点,顺次连接即可得;
(3)连接A′F′,利用勾股定理逆定理证△A′C′F′为等腰直角三角形即可得.
解答 解:(1)△A′B′C′即为所求;
(2)△D′E′F′即为所求;
(3)如图,连接A′F′,
∵△ABC≌△A′B′C′、△DEF≌△D′E′F′,
∴∠C+∠E=∠A′C′B′+∠D′E′F′=∠A′C′F′,
∵A′C′=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$、A′F′=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,C′F′=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,
∴A′C′2+A′F′2=5+5=10=C′F′2,
∴△A′C′F′为等腰直角三角形,
∴∠C+∠E=∠A′C′F′=45°,
故答案为:45°.
点评 本题主要考查作图-平移变换、轴对称变换,熟练掌握平移变换、轴对称变换及勾股定理逆定理是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.将一张矩形纸片按图1、图2所示依次对折两次,然后在图3中沿虚线剪开,得到①和②两部分,将①展开后,得到的平面图形一定是( )
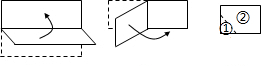

| A. | 直角三角形 | B. | 矩形 | C. | 菱形 | D. | 正方形 |
20.计算:($\frac{1}{3}$)2•3-1=( )
| A. | $\frac{1}{3}$ | B. | 1 | C. | $\frac{1}{27}$ | D. | -$\frac{1}{27}$ |
4.下列一元二次方程没有实数根的是( )
| A. | x2-2x=0 | B. | x2-1=0 | C. | x2+x+1=0 | D. | x2+2x+1=0 |
1.慈溪,因治南有溪而得名,慈溪的常住人口约为1460000人,1460000用科学记数法表示为( )
| A. | 0.146×107 | B. | 1.46×105 | C. | 14.6×105 | D. | 1.46×106 |
2.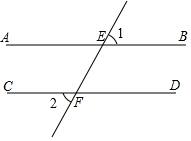 如图,AB∥CD,直线l交AB于点E,交CD于点F,若∠1=60°,则∠2等于( )
如图,AB∥CD,直线l交AB于点E,交CD于点F,若∠1=60°,则∠2等于( )
 如图,AB∥CD,直线l交AB于点E,交CD于点F,若∠1=60°,则∠2等于( )
如图,AB∥CD,直线l交AB于点E,交CD于点F,若∠1=60°,则∠2等于( )| A. | 120° | B. | 30° | C. | 40° | D. | 60° |
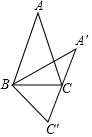 如图,在△ABC中,AB=AC,将△ABC绕顶点B顺时针旋转,得到△A′BC′.设∠A=α,当A′C′恰好经过顶点C时,∠A′BC=90°-$\frac{3α}{2}$(用含α的式子表示).
如图,在△ABC中,AB=AC,将△ABC绕顶点B顺时针旋转,得到△A′BC′.设∠A=α,当A′C′恰好经过顶点C时,∠A′BC=90°-$\frac{3α}{2}$(用含α的式子表示). 如图,在△ABC中,∠C=75°,将△ABC绕点A顺时针旋转到△ADE的位置,点E恰好落在边BC上,且AD∥BC,则∠D的度数为30°.
如图,在△ABC中,∠C=75°,将△ABC绕点A顺时针旋转到△ADE的位置,点E恰好落在边BC上,且AD∥BC,则∠D的度数为30°.