题目内容
矩形ABCD沿对角线BD折叠，点C落在点F，若AB=2，BC=4，则BE的长是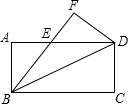
- A.
- B.
- C.2
- D.1
A
分析：由折叠性质和矩形的性质可知，∠EBD=∠CBD=∠EDB，即△BDE为等腰三角形，设BE=x，则AE=4-x，把问题转化到Rt△ABE中，由勾股定理求解．
解答：由折叠性质可知，∠EBD=∠CBD，
由矩形性质可知，∠EDB=∠CBD，
∴∠EBD=∠EDB，即BE=ED，设BE=x，则AE=4-x，
在Rt△ABE中，由勾股定理得：AB2+AE2=BE2，
即22+（4-x）2=x2，
解得x=即AE=．故选A．
点评：本题考查图形的翻折变换，解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变，如本题中折叠前后对应线段、角相等．
分析：由折叠性质和矩形的性质可知，∠EBD=∠CBD=∠EDB，即△BDE为等腰三角形，设BE=x，则AE=4-x，把问题转化到Rt△ABE中，由勾股定理求解．
解答：由折叠性质可知，∠EBD=∠CBD，
由矩形性质可知，∠EDB=∠CBD，
∴∠EBD=∠EDB，即BE=ED，设BE=x，则AE=4-x，
在Rt△ABE中，由勾股定理得：AB2+AE2=BE2，
即22+（4-x）2=x2，
解得x=
即AE=．故选A．点评：本题考查图形的翻折变换，解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变，如本题中折叠前后对应线段、角相等．
练习册系列答案
相关题目
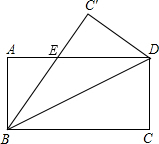如图将矩形ABCD沿对角线BD折叠，使C落在C′处，BC′交AD于点E，则下到结论不一定成立的是（ ）| A、AD=BC′ | ||
| B、∠EBD=∠EDB | ||
| C、△ABE∽△CBD | ||
D、sin∠ABE=
|
23、将矩形ABCD沿对角线BD折叠，使C落在F处，BF交AD于E，求证重合部分三角形BED是等腰三角形．
如图，将矩形ABCD沿对角线AC剪刀，再把△ACD沿CA方向平移得到△A1C1D1
（2013•荆州）如图，将矩形ABCD沿对角线AC剪开，再把△ACD沿CA方向平移得到△A1C1D1，连结AD1、BC1．若∠ACB=30°，AB=1，CC1=x，△ACD与△A1C1D1重叠部分的面积为s，则下列结论：