题目内容
23、将矩形ABCD沿对角线BD折叠，使C落在F处，BF交AD于E，求证重合部分三角形BED是等腰三角形．分析：由轴对称的性质可知∠EBD=∠CBD，由AD∥BC可得∠EDB=∠CBD，等量代换得∠EBD=∠EDB．
解答：证明：由折叠的性质可知∠EBD=∠CBD，
∵AD∥BC，
∴∠EDB=∠CBD，
∴∠EBD=∠EDB，
∴BE=ED，即△BED是等腰三角形．
∵AD∥BC，
∴∠EDB=∠CBD，
∴∠EBD=∠EDB，
∴BE=ED，即△BED是等腰三角形．
点评：本题考查图形的翻折变换，解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变，如本题中折叠前后角相等．
练习册系列答案
相关题目
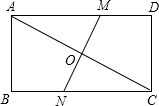矩形ABCD的边AB=4，AD=8，将这个矩形沿折痕MN对折，使两对角顶点中的A点恰好落在C点的位置，求AM的长．
8、如图，将矩形纸片ABCD沿BD对折，使点C落在E处，BE与AD相交于点O，写出一组相等线段、相等角（不包括矩形的对边、对角）
矩形ABCD的边AB=4，AD=8，将这个矩形沿折痕MN对折，使两对角顶点中的A点恰好落在C点的位置，求AM的长．
