题目内容
 (2013•荆州)如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连结AD1、BC1.若∠ACB=30°,AB=1,CC1=x,△ACD与△A1C1D1重叠部分的面积为s,则下列结论:
(2013•荆州)如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连结AD1、BC1.若∠ACB=30°,AB=1,CC1=x,△ACD与△A1C1D1重叠部分的面积为s,则下列结论:①△A1AD1≌△CC1B;
②当x=1时,四边形ABC1D1是菱形;
③当x=2时,△BDD1为等边三角形;
④s=
| ||
| 8 |
其中正确的是
①②③④
①②③④
(填序号).分析:①根据矩形的性质,得∠DAC=∠ACB,再由平移的性质,可得出∠A1=∠ACB,A1D1=CB,从而证出结论;
②根据菱形的性质,四条边都相等,可推得当C1在AC中点时四边形ABC1D1是菱形.
③当x=2时,点C1与点A重合,可求得BD=DD1=BD1=2,从而可判断△BDD1为等边三角形.
④易得△AC1F∽△ACD,根据面积比等于相似比平方可得出s与x的函数关系式..
②根据菱形的性质,四条边都相等,可推得当C1在AC中点时四边形ABC1D1是菱形.
③当x=2时,点C1与点A重合,可求得BD=DD1=BD1=2,从而可判断△BDD1为等边三角形.
④易得△AC1F∽△ACD,根据面积比等于相似比平方可得出s与x的函数关系式..
解答:解①∵四边形ABCD为矩形,
∴BC=AD,BC∥AD
∴∠DAC=∠ACB
∵把△ACD沿CA方向平移得到△A1C1D1,
∴∠A1=∠DAC,A1D1=AD,AA1=CC1,
在△A1AD1与△CC1B中,
,
∴△A1AD1≌△CC1B(SAS),
故①正确;
②∵∠ACB=30°,
∴∠CAB=60°,
∵AB=1,
∴AC=2,
∵x=1,
∴AC1=1,
∴△AC1B是等边三角形,
∴AB=BC1,
又AB∥BC1,
∴四边形ABC1D1是菱形,
故②正确;
③如图所示:
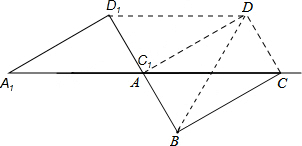
则可得BD=DD1=BD1=2,
∴△BDD1为等边三角形,故③正确.
④易得△AC1F∽△ACD,
∴
=(
)2,
解得:S△AC1F=
(x-2)2 (0<x<2);故④正确;
综上可得正确的是①②③④.
故答案为:①②③④.
∴BC=AD,BC∥AD
∴∠DAC=∠ACB
∵把△ACD沿CA方向平移得到△A1C1D1,
∴∠A1=∠DAC,A1D1=AD,AA1=CC1,
在△A1AD1与△CC1B中,
|
∴△A1AD1≌△CC1B(SAS),
故①正确;
②∵∠ACB=30°,
∴∠CAB=60°,
∵AB=1,
∴AC=2,
∵x=1,
∴AC1=1,
∴△AC1B是等边三角形,
∴AB=BC1,
又AB∥BC1,
∴四边形ABC1D1是菱形,
故②正确;
③如图所示:

则可得BD=DD1=BD1=2,
∴△BDD1为等边三角形,故③正确.
④易得△AC1F∽△ACD,
∴
| S△AC1F |
| S△ACD |
| 2-x |
| 2 |
解得:S△AC1F=
| ||
| 8 |
综上可得正确的是①②③④.
故答案为:①②③④.
点评:本题考查了相似三角形的判定与性质、矩形的性质、等边三角形的判定及解直角三角形的知识,解答本题需要我们熟练掌握全等三角形的判定及含30°角的直角三角形的性质,有一定难度.

练习册系列答案
相关题目
 (2013•荆州)如图,AB∥CD,∠ABE=60°,∠D=50°,则∠E的度数为( )
(2013•荆州)如图,AB∥CD,∠ABE=60°,∠D=50°,则∠E的度数为( )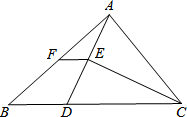 (2013•荆州)如图,在△ABC中,BC>AC,点D在BC上,且DC=AC,∠ACB的平分线CE交AD于E,点F是AB的中点,则S△AEF:S四边形BDEF为( )
(2013•荆州)如图,在△ABC中,BC>AC,点D在BC上,且DC=AC,∠ACB的平分线CE交AD于E,点F是AB的中点,则S△AEF:S四边形BDEF为( ) (2013•荆州)如图,将含60°角的直角三角板ABC绕顶点A顺时针旋转45°度后得到△AB′C′,点B经过的路径为弧BB′,若∠BAC=60°,AC=1,则图中阴影部分的面积是( )
(2013•荆州)如图,将含60°角的直角三角板ABC绕顶点A顺时针旋转45°度后得到△AB′C′,点B经过的路径为弧BB′,若∠BAC=60°,AC=1,则图中阴影部分的面积是( ) (2013•荆州)如图,在平面直角坐标系中,直线y=-3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限作正方形ABCD,点D在双曲线
(2013•荆州)如图,在平面直角坐标系中,直线y=-3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限作正方形ABCD,点D在双曲线 (2013•荆州)如图,在高度是21米的小山A处测得建筑物CD顶部C处的仰角为30°,底部D处的俯角为45°,则这个建筑物的高度CD=
(2013•荆州)如图,在高度是21米的小山A处测得建筑物CD顶部C处的仰角为30°,底部D处的俯角为45°,则这个建筑物的高度CD=