题目内容
3.飞马汽车销售公司3月份销售新上市一种新型低能耗汽车8辆,由于该型汽车的优越的经济适用性,销量快速上升,5月份该公司销售该型汽车达18辆.(1)求该公司销售该型汽车4月份和5月份的平均增长率;
(2)该型汽车每辆的进价为9万元,该公司的该型车售价为9.8万元/辆.且销售m辆汽车,汽车厂返利销售公司0.04m万元/辆.若使6月份每辆车盈利不低于1.7万元,那么该公司6月份至少需要销售该型汽车多少辆?(盈利=销售利润+返利)
分析 (1)设该公司销售该型汽车4月份和5月份的平均增长率为x,根据3月份和5月份的销售量,即可得出关于x的一元二次方程,解之取其正值即可;
(2)根据盈利=销售利润+返利结合每辆车盈利不低于1.7万元,即可得出关于m的一元一次不等式,解之即可得出m的取值范围,再取其内的最小正整数即可.
解答 解:(1)设该公司销售该型汽车4月份和5月份的平均增长率为x,
根据题意得:8(1+x)2=18,
解得:x1=-2.50(不合题意,舍去),x2=0.5=50%.
答:该公司销售该型汽车4月份和5月份的平均增长率为50%.
(2)根据题意得:9.8-9+0.04m≥1.7,
解得:m≥22.5,
∵m为正整数,
∴该公司6月份至少需要销售该型汽车23辆.
点评 本题考查了分式方程的应用以及一元一次不等式的应用,解题的关键是:(1)找准等量关系,列出关于x的一元二次方程:(2)根据盈利=销售利润+返利,列出关于m的一元一次不等式.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
 如图,在?ABCD中,E是AD上一点,且AD=3AE,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,$\overrightarrow{BE}$=-$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$.(结果用$\overrightarrow{a}$、$\overrightarrow{b}$表示)
如图,在?ABCD中,E是AD上一点,且AD=3AE,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,$\overrightarrow{BE}$=-$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$.(结果用$\overrightarrow{a}$、$\overrightarrow{b}$表示)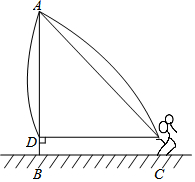 想测量旗杆高度,一个绳子拴在旗杆的顶端自然垂落多了1米,一个小孩把绳子水平拉开5米使绳子被拉直,此时绳子底部距地面1米,问:旗杆多高?
想测量旗杆高度,一个绳子拴在旗杆的顶端自然垂落多了1米,一个小孩把绳子水平拉开5米使绳子被拉直,此时绳子底部距地面1米,问:旗杆多高?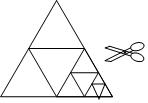 在一次数学综合实践课上,某同学将一张等边三角形纸片沿中位线剪成4个小三角形.称为第一次操作;然后,将其中的一个三角形按同样方式再剪成4个小三角形,共得到7个小三角形,称为第二次操作;再将其中一个三角形按同样方式再剪成4个小三角形,共得到10个小三角形,称为第三次操作;…根据以上操作,若要得到100个小三角形,则需要操作的次数是( )
在一次数学综合实践课上,某同学将一张等边三角形纸片沿中位线剪成4个小三角形.称为第一次操作;然后,将其中的一个三角形按同样方式再剪成4个小三角形,共得到7个小三角形,称为第二次操作;再将其中一个三角形按同样方式再剪成4个小三角形,共得到10个小三角形,称为第三次操作;…根据以上操作,若要得到100个小三角形,则需要操作的次数是( )