题目内容
20. 一次函数y=kx+b的图象在坐标系中的位置如图所示.
一次函数y=kx+b的图象在坐标系中的位置如图所示.(1)证明:关于x的一元二次方程x2+3x+k-1=0必有两个不等实根;
(2)设直线y=kx+b与y轴交于点A,与x轴交于点B,AO=BO=4,在线段AB上是否存在点P,使OP=$\sqrt{10}$?若存在,求点P的坐标,若不存在,说明理由.
分析 (1)先计算判别式的值得到△=13-4k,再利用一次函数的图象与系数的关系得到k<0,则可判断△>0,于是根据判别式的意义可得到结论;
(2)先利用待定系数法求出一次函数解析式为y=-x+4,利用一次函数图象上点的坐标特征,设P(t,-t+4),利用两点间的距离公式得到$\sqrt{{t}^{2}+(-t+4)^{2}}$=$\sqrt{10}$,然后解方程求出t即可得到P点坐标.
解答 (1)证明:△=32-4(k-1)=13-4k,
∵一次函数y=kx+b的图象经过第一、二、四象限,
∴k<0,
∴△>0,
∴关于x的一元二次方程x2+3x+k-1=0必有两个不等实根;
(2)存在.
∵AO=BO=4,
∴A(0,4),B(4,0),
把A(0,4),B(4,0)代入y=kx+b得$\left\{\begin{array}{l}{b=4}\\{4k+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-1}\\{b=4}\end{array}\right.$,
∴一次函数解析式为y=-x+4,
设P(t,-t+4),
∴OP=$\sqrt{{t}^{2}+(-t+4)^{2}}$,
而OP=$\sqrt{10}$,
∴$\sqrt{{t}^{2}+(-t+4)^{2}}$=$\sqrt{10}$,
整理得t2-4t+3=0,解得t1=1,t2=3,
∴P点坐标为(1,3)或(3,1).
点评 本题考查了一次函数图象与系数的关系:对于y=kx+b与y轴交于(0,b),k>0,b>0?y=kx+b的图象在一、二、三象限;k>0,b<0?y=kx+b的图象在一、三、四象限;k<0,b>0?y=kx+b的图象在一、二、四象限;k<0,b<0?y=kx+b的图象在二、三、四象限.也考查了判别式的意义.

 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案 如图,AC=2AB,D是AC中点,E是AD中点,点F在BE延长线上,且BE=EF,求证:BC=2EF,∠F=∠C.
如图,AC=2AB,D是AC中点,E是AD中点,点F在BE延长线上,且BE=EF,求证:BC=2EF,∠F=∠C.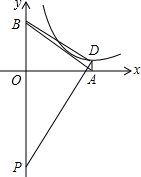 如图,在平面直角坐标系中,直线y=-$\frac{3}{4}$x+6与x轴、y轴的正半轴分别相交于点A,B两点,点D在反比例函数y=$\frac{k}{x}$(k>0)的图象上,DA⊥OA,点P在y轴负半轴上,OP=14.
如图,在平面直角坐标系中,直线y=-$\frac{3}{4}$x+6与x轴、y轴的正半轴分别相交于点A,B两点,点D在反比例函数y=$\frac{k}{x}$(k>0)的图象上,DA⊥OA,点P在y轴负半轴上,OP=14.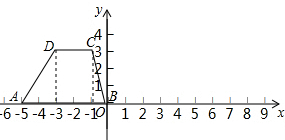 如图所示.
如图所示.