Question

【题目】已知：如图△ABC内接于⊙O，OH⊥AC于H，过A点的切线与OC的延长线交于点D，∠B＝30°，OH＝5．

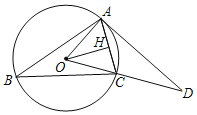
（1）求⊙O的半径；

（2）求出劣弧AC的长（结果保留π）．

Answer 1

【答案】（1）⊙O的半径为10；（2）劣弧AC的长为．

【解析】

（1）求出∠AOC＝2∠B＝60°，由等腰三角形的性质知∠AOH＝30°，故可由余弦的概念求出AO的值；

（2）根据弧长公式求劣弧AC的长．

（1）∵∠AOC＝2∠B，∠B＝30°，

∴∠AOC＝60°，

∵OH⊥AC，OA＝OC，

∴OH是等腰三角形AOC的底边AC上的高，

∴∠AOH＝∠AOC＝30°，

∴AO＝＝5×＝10，

即⊙O的半径为10；

（2）∵⊙O的半径为10，∠AOC＝60°，

∴劣弧AC的长为：．