题目内容
 如图矩形ABCD中,AB=2,点E在BC上并且AE=EC,若将矩形纸片沿AE折叠,使点B恰好落在AC上,则矩形ABCD的面积为
如图矩形ABCD中,AB=2,点E在BC上并且AE=EC,若将矩形纸片沿AE折叠,使点B恰好落在AC上,则矩形ABCD的面积为
- A.

- B.2

- C.4

- D.6

B
分析:根据折叠的性质及等边对等角的性质,可得到∠BAE=∠EAC=∠ECA,根据三角形内角和定理即可求得∠ECA的度数,再根据直角三角形的性质可求得AC的长,在Rt△ABC中利用勾股定理可求出BC的长,根据矩形的面积公式即可得出结论.
解答:∵AE=EC,
∴∠EAC=∠ECA,
∵将纸片沿AE折叠,点B恰好落在AC上,
∴∠BAE=∠EAC,
∴∠BAE=∠EAC=∠ECA,
∵∠B+∠ECA+∠CAB=180°,
∴∠ECA=30°,
∵AB=2,
∴AC=2AB=4,
在Rt△ABC中,
∵AB2+BC2=AC2,即22+BC2=42,解得BC=2 ,
,
∴S矩形ABCD= AB•BC=
AB•BC= ×2×2
×2×2 =2
=2 .
.
故选B.
点评:本题考查的是图形的反折变换及矩形的性质,熟知图形反折不变性的性质是解答此题的关键.
分析:根据折叠的性质及等边对等角的性质,可得到∠BAE=∠EAC=∠ECA,根据三角形内角和定理即可求得∠ECA的度数,再根据直角三角形的性质可求得AC的长,在Rt△ABC中利用勾股定理可求出BC的长,根据矩形的面积公式即可得出结论.
解答:∵AE=EC,
∴∠EAC=∠ECA,
∵将纸片沿AE折叠,点B恰好落在AC上,
∴∠BAE=∠EAC,
∴∠BAE=∠EAC=∠ECA,
∵∠B+∠ECA+∠CAB=180°,
∴∠ECA=30°,
∵AB=2,
∴AC=2AB=4,
在Rt△ABC中,
∵AB2+BC2=AC2,即22+BC2=42,解得BC=2
 ,
,∴S矩形ABCD=
 AB•BC=
AB•BC= ×2×2
×2×2 =2
=2 .
.故选B.
点评:本题考查的是图形的反折变换及矩形的性质,熟知图形反折不变性的性质是解答此题的关键.

练习册系列答案
相关题目
 14、如图矩形ABCD中BC=8,AB=4,将矩形纸片沿对角线对折,使C点落在F处,BC与AD边交于点E,则下列四个结论中:
14、如图矩形ABCD中BC=8,AB=4,将矩形纸片沿对角线对折,使C点落在F处,BC与AD边交于点E,则下列四个结论中: 如图矩形ABCD中,E为BC上一点,DF⊥AE于F.
如图矩形ABCD中,E为BC上一点,DF⊥AE于F. 29、如图矩形ABCD中,DP平分∠ADC交BC于P点,将一个直角三角板的直角顶点放在P点处,且使它的一条直角边过A点,另一条直角边交CD于E.找出图中与PA相等的线段.并说明理由.
29、如图矩形ABCD中,DP平分∠ADC交BC于P点,将一个直角三角板的直角顶点放在P点处,且使它的一条直角边过A点,另一条直角边交CD于E.找出图中与PA相等的线段.并说明理由. 如图矩形ABCD中,过A,B两点的⊙O切CD于E,交BC于F,AH⊥BE于H,连接EF.
如图矩形ABCD中,过A,B两点的⊙O切CD于E,交BC于F,AH⊥BE于H,连接EF.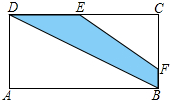 如图矩形ABCD中,AB=8cm,CB=4cm,E是DC的中点,BF=
如图矩形ABCD中,AB=8cm,CB=4cm,E是DC的中点,BF=