题目内容
 如图矩形ABCD中,E为BC上一点,DF⊥AE于F.
如图矩形ABCD中,E为BC上一点,DF⊥AE于F.(1)求证:△ABE∽△DFA;
(2)若AB=6,AD=12,BE=8,求DF的长.
分析:(1)△ABE和△DFA都是直角三角形,还需一对角对应相等即可.根据AD∥BC可得∠DAF=∠AEB,问题得证;
(2)运用相似三角形的性质求解.
(2)运用相似三角形的性质求解.
解答:(1)证明:∵DF⊥AE,∴∠AFD=90°. (1分)
∴∠B=∠AFD=90°. (2分)
又∵AD∥BC,
∴∠DAE=∠AEB. (3分)
∴△ABE∽△DFA. (4分)
(2)解:∵AB=6,BE=8,∠B=90°,
∴AE=10. (6分)
∵△ABE∽△DFA,∴
=
. (7分)
即
=
.
∴DF=7.2. (8分)
∴∠B=∠AFD=90°. (2分)
又∵AD∥BC,
∴∠DAE=∠AEB. (3分)
∴△ABE∽△DFA. (4分)
(2)解:∵AB=6,BE=8,∠B=90°,
∴AE=10. (6分)
∵△ABE∽△DFA,∴
| AB |
| DF |
| AE |
| AD |
即
| 6 |
| DF |
| 10 |
| 12 |
∴DF=7.2. (8分)
点评:此题考查了相似三角形的判定和性质,以及矩形的性质、勾股定理等知识点,难度中等.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 14、如图矩形ABCD中BC=8,AB=4,将矩形纸片沿对角线对折,使C点落在F处,BC与AD边交于点E,则下列四个结论中:
14、如图矩形ABCD中BC=8,AB=4,将矩形纸片沿对角线对折,使C点落在F处,BC与AD边交于点E,则下列四个结论中: 29、如图矩形ABCD中,DP平分∠ADC交BC于P点,将一个直角三角板的直角顶点放在P点处,且使它的一条直角边过A点,另一条直角边交CD于E.找出图中与PA相等的线段.并说明理由.
29、如图矩形ABCD中,DP平分∠ADC交BC于P点,将一个直角三角板的直角顶点放在P点处,且使它的一条直角边过A点,另一条直角边交CD于E.找出图中与PA相等的线段.并说明理由. 如图矩形ABCD中,过A,B两点的⊙O切CD于E,交BC于F,AH⊥BE于H,连接EF.
如图矩形ABCD中,过A,B两点的⊙O切CD于E,交BC于F,AH⊥BE于H,连接EF.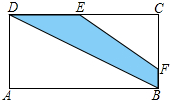 如图矩形ABCD中,AB=8cm,CB=4cm,E是DC的中点,BF=
如图矩形ABCD中,AB=8cm,CB=4cm,E是DC的中点,BF=