题目内容
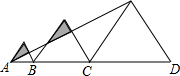 已知三个边长分别为2、3、5的正三角形从左到右如图排列,则图中阴影部分面积为
已知三个边长分别为2、3、5的正三角形从左到右如图排列,则图中阴影部分面积为考点:相似三角形的判定与性质,等边三角形的性质
专题:
分析:如图,可证明AG⊥EB,AG⊥FC,再结合等边三角形的性质,可求得EM=
EB,AM=
EB,在Rt△FNH中可求得FN=1,同理可求得FH,NH,利用三角形的面积公式可求得阴影部分面积.
| 1 |
| 2 |
| ||
| 2 |
解答: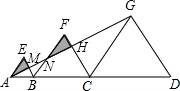 解:
解:
如图,设AC交BE、BF、CF于点M、N、H,
∵AB=2,BC=3,CG=5,
∴AC=CG,
∴∠CAG=∠AGC=30°,
∴AG⊥BE,
又∵∠EBA=∠FCA=60°,
∴EB∥FC.
∴AG⊥CF,
在Rt△AEM中,AE=2,EM=
AE=1,AM=
AE=
,
∴S△AEM=
EM•AM=
×1×
=
,
又同理可得到AB=BN=2,
∴FN=1,
在Rt△FNH中,FH=
FN=
,NH=
FN=
,
∴S△FNH=
FH•NH=
×
×
=
,
∴S阴影=S△AEM+S△FNH=
+
=
.
故答案为:
.
 解:
解:如图,设AC交BE、BF、CF于点M、N、H,
∵AB=2,BC=3,CG=5,
∴AC=CG,
∴∠CAG=∠AGC=30°,
∴AG⊥BE,
又∵∠EBA=∠FCA=60°,
∴EB∥FC.
∴AG⊥CF,
在Rt△AEM中,AE=2,EM=
| 1 |
| 2 |
| ||
| 2 |
| 3 |
∴S△AEM=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
又同理可得到AB=BN=2,
∴FN=1,
在Rt△FNH中,FH=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
∴S△FNH=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 8 |
∴S阴影=S△AEM+S△FNH=
| ||
| 2 |
| ||
| 8 |
5
| ||
| 8 |
故答案为:
5
| ||
| 8 |
点评:本题主要考查等边三角形的性质及含30度角的直角三角形的性质,根据条件证得AG⊥EB,AG⊥FC是解题的关键.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
下列命题是假命题的是( )
| A、两点之间,线段最短 |
| B、过不在同一直线上的三点有且只有一个圆 |
| C、一组对应边相等的两个等边三角形全等 |
| D、对角线相等的四边形是矩形 |
 如图是某地一座抛物线形拱桥,桥拱在竖直平面内,与水面相交于A,B两点,拱桥最高点C到AB的距离为9m,AB=36m,D,E为拱桥底部的两点,且DE∥AB,点E到直线AB的距离为7m.建立平面直角坐标系,求:
如图是某地一座抛物线形拱桥,桥拱在竖直平面内,与水面相交于A,B两点,拱桥最高点C到AB的距离为9m,AB=36m,D,E为拱桥底部的两点,且DE∥AB,点E到直线AB的距离为7m.建立平面直角坐标系,求:
 某反比例函数y=
某反比例函数y=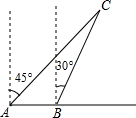 如图所示,一渔船正以每小时30海里的速度由西向东航行,在A处看见小岛C在船的北偏东45°方向上.40min后,渔船行至B处,此时看见小岛C在船的北偏东30°.若以小岛C为中心周围30海里是危险区,问这艘渔船继续向东航行是否有进入危险区的可能?
如图所示,一渔船正以每小时30海里的速度由西向东航行,在A处看见小岛C在船的北偏东45°方向上.40min后,渔船行至B处,此时看见小岛C在船的北偏东30°.若以小岛C为中心周围30海里是危险区,问这艘渔船继续向东航行是否有进入危险区的可能?