题目内容
9.某地区为了进一步缓解交通拥堵问题,决定修建一条公路.在30≤x≤120范围内,如果平均每天的修建费y(万元)与修建天数x(天)之间具有一次函数的关系,如下表所示.| x | 50 | 60 | 90 | 120 |
| y | 40 | 38 | 32 | 26 |
(2)如果修建40天,那么平均每天的修建费是多少?
分析 (1)利用待定系数法求出一次函数解析式,进而得出答案;
(2)利用(1)中所求解析式进而得出平均每天的修建费.
解答 解:(1)设y关于x的函数解析式为:y=kx+b,
则$\left\{\begin{array}{l}{50k+b=40}\\{60k+b=38}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{1}{5}}\\{b=50}\end{array}\right.$,
故y关于x的函数解析式为:y=-$\frac{1}{5}$x+50;
(2)由(1)得:y=-$\frac{1}{5}$×40+50=42(万元),
答:平均每天的修建费是42万元.
点评 此题主要考查了一次函数的应用,利用待定系数法求出一次函数解析式是解题关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
20.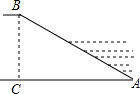 如图所示,河堤横断面迎水坡AB的坡比是1:2,堤高BC=5m,则坡面AB的长度是
如图所示,河堤横断面迎水坡AB的坡比是1:2,堤高BC=5m,则坡面AB的长度是
( )
 如图所示,河堤横断面迎水坡AB的坡比是1:2,堤高BC=5m,则坡面AB的长度是
如图所示,河堤横断面迎水坡AB的坡比是1:2,堤高BC=5m,则坡面AB的长度是( )
| A. | 10m | B. | 10$\sqrt{5}$m | C. | 15m | D. | 5$\sqrt{5}$m |
1.已知|a|=3,|b|=4,且ab<0,则a-b的值为( )
| A. | 1或7个 | B. | 1-或7 | C. | ±1个 | D. | ±7 |
 如图,△ABC≌△DBC,∠A=110°,则∠D=110°.
如图,△ABC≌△DBC,∠A=110°,则∠D=110°. 过线段AB上的一点P作线段AB的垂线.(保留作图痕迹,不写作法)
过线段AB上的一点P作线段AB的垂线.(保留作图痕迹,不写作法)