题目内容
3.a14不可以写成( )| A. | a7•a7 | B. | (-a)2•a3•a4•a5 | C. | -a4•(-a)4•(-a)3•(-a)3 | D. | a5•a9 |
分析 利用乘方的性质以及同底数的幂的乘法法则即可求解每个式子,从而判断.
解答 解:A、a7•a7=a 7+7=a14,则选项不符合题意;
B、原式=a2•a3•a4•a5=a 2+3+4+5=a14,则选项不符合题意;
C、原式=-a4•a4•(-a3)•(-a3)=-a4•a4•a3•a3=-a14,则选项符合题意;
D、a5•a9=a5+9=a14,选项不符合题意.
故选C.
点评 本题考查了乘方的性质以及同底数的幂的乘法法则,理解乘方的性质,确定结果的符号是关键.

练习册系列答案
相关题目
6.直线y=2x-3与y=-x+3的交点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
7.下列运算正确的是( )
| A. | (a3)2=a5 | B. | a2•a3=a5 | C. | a6÷a2=a3 | D. | 3a2-2a2=1 |
4.在平行四边形ABCD中,∠A的平分线把BC边分成长度是3和4的两部分,则平行四边形ABCD周长是( )
| A. | 22 | B. | 20 | C. | 22或20 | D. | 18 |
8.若关于x的一元二次方程(k-1)x2+2x-2=0有两个不相等的实数根,则k的取值范围是( )
| A. | k>$\frac{1}{2}$ | B. | k≥$\frac{1}{2}$ | C. | k>$\frac{1}{2}$且k≠1 | D. | k≥$\frac{1}{2}$且k≠1 |
15.一次函数y=kx-k(k>0)的图象大致是( )
| A. |  | B. |  | C. |  | D. |  |
12.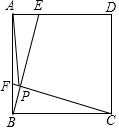 如图,点E、F是边长为4的正方形ABCD边AD、AB上的动点,且AF=DE,BE交CF于点P,在点E、F运动的过程中,PA的最小值为( )
如图,点E、F是边长为4的正方形ABCD边AD、AB上的动点,且AF=DE,BE交CF于点P,在点E、F运动的过程中,PA的最小值为( )
 如图,点E、F是边长为4的正方形ABCD边AD、AB上的动点,且AF=DE,BE交CF于点P,在点E、F运动的过程中,PA的最小值为( )
如图,点E、F是边长为4的正方形ABCD边AD、AB上的动点,且AF=DE,BE交CF于点P,在点E、F运动的过程中,PA的最小值为( )| A. | 2 | B. | 2$\sqrt{2}$ | C. | 4$\sqrt{2}$-2 | D. | 2$\sqrt{5}$-2 |
13.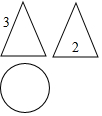 如图是一个几何体的三视图(图中尺寸单位:cm),根据图中所示数据计算这个几何体的侧面积为( )cm2.
如图是一个几何体的三视图(图中尺寸单位:cm),根据图中所示数据计算这个几何体的侧面积为( )cm2.
 如图是一个几何体的三视图(图中尺寸单位:cm),根据图中所示数据计算这个几何体的侧面积为( )cm2.
如图是一个几何体的三视图(图中尺寸单位:cm),根据图中所示数据计算这个几何体的侧面积为( )cm2.| A. | 3π | B. | 6π | C. | 9π | D. | 12π |