题目内容
已知CD是经过∠BCA顶点C的一条直线,CA=CB.E、F分别是直线CD上两点,且∠BEC=∠CFA=∠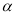 .
.
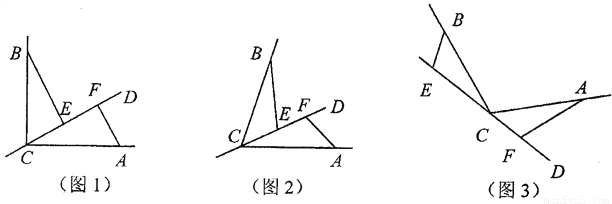
(1)若直线CD经过∠BCA的内部,且E、F在射线CD上,请解决下面问题:
①如图1若∠BCA=90°,∠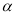 =90°、探索三条线段EF、BE、AF的数量关系并证明你的结论.
=90°、探索三条线段EF、BE、AF的数量关系并证明你的结论.
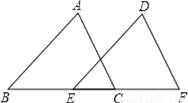
②如图2,若0°<∠BCA<180°, 请添加一个关于∠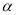 与∠BCA关系的条件___ ____使①中的结论仍然成立;
与∠BCA关系的条件___ ____使①中的结论仍然成立;
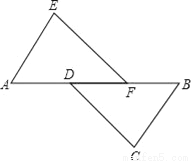
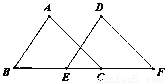
(2)如图3,若直线CD经过∠BCA的外部,∠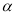 =∠BCA,请写出三条线段EF、BE、AF的数量关系并证明你的结论.
=∠BCA,请写出三条线段EF、BE、AF的数量关系并证明你的结论.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


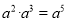 B.
B. 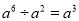
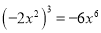 D.
D. 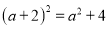
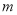 ,7)与点B(8,
,7)与点B(8, 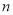 )关于
)关于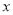 轴对称,则
轴对称,则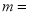 ________________.
________________.