题目内容
 如图,在△ABC中,AC=8,BC=6,DE是△ABD的边AB上的高,且DE=4,AD=2
如图,在△ABC中,AC=8,BC=6,DE是△ABD的边AB上的高,且DE=4,AD=2| 5 |
| 5 |
考点:勾股定理,勾股定理的逆定理
专题:
分析:先根据勾股定理求出AE和BE,求出AB,根据勾股定理的逆定理求出△ABC是直角三角形,再求出面积即可.
解答:解:∵DE是AB边上的高,
∴∠AED=∠BED=90°,
在Rt△ADE中,由勾股定理得:AE=
=
=2,
同理:在Rt△BDE中,由勾股定理得:BE=8,
∴AB=2+8=10,
在△ABC中,由AB=10,AC=8,BC=6,
得:AB2=AC2+BC2
∴△ABC是直角三角形
∴△ABC的面积是
×AC×BC=
×8×6=24.
∴∠AED=∠BED=90°,
在Rt△ADE中,由勾股定理得:AE=
| AD2-DE2 |
(2
|
同理:在Rt△BDE中,由勾股定理得:BE=8,
∴AB=2+8=10,
在△ABC中,由AB=10,AC=8,BC=6,
得:AB2=AC2+BC2
∴△ABC是直角三角形
∴△ABC的面积是
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了三角形面积,勾股定理的逆定理,勾股定理的应用,注意:在直角三角形中,两直角边的平方和等于斜边的平方.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 尺规作图(不写作法,仅保留作图痕迹,在原图上不给分):
尺规作图(不写作法,仅保留作图痕迹,在原图上不给分): 在正方形网格中,每个小正方形的顶点称为格点,以格点连线为边的三角形叫做格点三角形,如图1、图2中的△ABC和△DEF都是格点三角形.
在正方形网格中,每个小正方形的顶点称为格点,以格点连线为边的三角形叫做格点三角形,如图1、图2中的△ABC和△DEF都是格点三角形. 如图,长和宽分别是a、b的长方形纸片的四个角都剪去一个边长为x的正方形.
如图,长和宽分别是a、b的长方形纸片的四个角都剪去一个边长为x的正方形.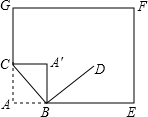 如图,将书页一角斜折过去,使角的顶点A落在A′处,BC为折痕,BD平分∠A′BE,求∠CBD的度数.
如图,将书页一角斜折过去,使角的顶点A落在A′处,BC为折痕,BD平分∠A′BE,求∠CBD的度数.