题目内容
5.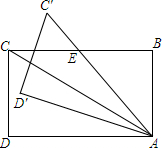 如图,矩形ABCD中,AB=$\sqrt{3}$,AD=3,将△ADC绕点A顺时针旋转α角(0°≤α≤90°)得到△AD′C′,且AC′与BC交于E.
如图,矩形ABCD中,AB=$\sqrt{3}$,AD=3,将△ADC绕点A顺时针旋转α角(0°≤α≤90°)得到△AD′C′,且AC′与BC交于E.(1)当α=15°时,求证:AB=BE;
(2)求旋转过程中边DC扫过的面积.
分析 (1)由于AB=$\sqrt{3}$,AD=3,可得∠CAB=60°,结论显然;
(2)画出图形,旋转过程中边DC扫过的面积就是两个扇形面积之差,这两个扇形面积都是四分之一圆的面积,且半径分别为AC、AD.
解答 解:(1)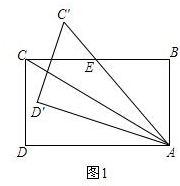
∵矩形ABCD中,AB=$\sqrt{3}$,AD=3,
∴tan∠CAB=$\frac{BC}{AB}$=$\frac{3}{\sqrt{3}}$=$\sqrt{3}$,
∴∠CAB=60°,
∵∠CAC'=15°,
∴∠EAB=45°,
∴△ABE是等腰直角三角形,
∴AB=BE;
(2)如图2,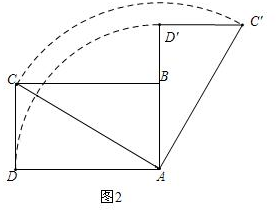
设旋转过程中边DC扫过的面积为S,
∵AB=$\sqrt{3}$,AD=3,
∴AC=2$\sqrt{3}$,
∴${S}_{扇形ADD'}=\frac{1}{4}π•A{D}^{2}$=$\frac{9}{4}π$,
${S}_{扇形ACC'}=\frac{1}{4}π•A{C}^{2}$=3π,
∴S=S扇形ADD'-S扇形ACC'=$\frac{3}{4}π$.
点评 本题考查了旋转的性质、矩形的性质、特殊角的三角函数、等腰直角三角形的判定性质、扇形面积计算等知识点,难度适中.注意旋转变换的“不变”特征,即旋转前后对应的线段和角度是不变的.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
13.下列命题中,真命题有( )个
①三角形有且只有一个外接圆,圆有且只有一个内接三角形;
②如果两条弧不等,那么它们所对的弦也不等;
③如果两条弦相等,那么它们所对的圆周角相等;
④如果两个圆心角相等,那么它们所对的弧相等.
①三角形有且只有一个外接圆,圆有且只有一个内接三角形;
②如果两条弧不等,那么它们所对的弦也不等;
③如果两条弦相等,那么它们所对的圆周角相等;
④如果两个圆心角相等,那么它们所对的弧相等.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
10.在数3.8,-(-10),2π,-|-$\frac{22}{7}$|,0,-22中,正数的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
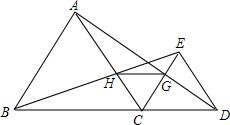 如图,已知点B、C、D在同一条直线上,△ABC和△ECD均是等边三角形.BE与AC交于点H,AD与CE交于点G.
如图,已知点B、C、D在同一条直线上,△ABC和△ECD均是等边三角形.BE与AC交于点H,AD与CE交于点G.