题目内容
19. 某商品每天的销售量P(件)与卖出价格x(元/件)的关系可以近似的看作一次函数关系;
某商品每天的销售量P(件)与卖出价格x(元/件)的关系可以近似的看作一次函数关系;(1)求P与x之间的函数关系式;
(2)如果这种商品的买入价为每件8元,试求每天的销售利润y(元)与卖出价格x(元/件)的函数关系式;(销售利润=销售收入-买入支出)
(3)在(2)的条件下,当卖出价格为多少时,能获最大利润?最大利润是多少?
分析 (1)设y与x之间的函数关系式为y=kx+b(k≠0),根据所给函数图象列出关于k、b的关系式,求出k、b的值即可;
(2)根据题意销售利润=销售收入-买入支出,代入数据即可得到结论;
(3)把每天的利润W与销售单价x之间的函数关系式化为二次函数顶点式的形式,由此关系式即可得出结论.
解答 解:(1)设p与x之间的函数关系式为p=kx+b(k≠0),由所给函数图象可知,
$\left\{\begin{array}{l}{5k+b=150}\\{10k+b=100}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-10}\\{b=200}\end{array}\right.$.
故y与x的函数关系式为p=-10x+200;
(2)∵p=-10x+200,
∴y=(x-8)p=(x-8)(-10x+200)
=-10x2+280x-1600
=-10(x-14)2+360,
∴销售利润y(元)与卖出价格x(元/件)的函数关系式y=-10(x-14)2+360,
(3)∵y=-10(x-14)2+360,a=-10<0,
∴当x=14时,y最大=360,
∴售价定为14元/件时,每天最大利润y=360元.
点评 本题考查的是二次函数的应用,根据题意列出关于k、b的关系式是解答此题的关键.

练习册系列答案
相关题目
11.下列四个数中,在-2到0之间的数是( )
| A. | -1 | B. | -3 | C. | 1 | D. | 3 |
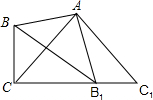 如图所示,∠BAB1=∠CAC1=90°,AB=AB1,AC=AC1,B1在CC1上.
如图所示,∠BAB1=∠CAC1=90°,AB=AB1,AC=AC1,B1在CC1上. 如图,直线y=kx+2与直线y=$\frac{1}{3}$x相交于点A(3,1),与x轴交于点B.
如图,直线y=kx+2与直线y=$\frac{1}{3}$x相交于点A(3,1),与x轴交于点B. 如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠ADB=108度.
如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠ADB=108度. 如图,王强在一次高尔夫球的练习中,在某处击球,其飞行路线满足抛物线y=-$\frac{1}{5}$x2+$\frac{8}{5}$x,其中y(m)是球飞行的高度,x(m)是球飞行的水平距离.
如图,王强在一次高尔夫球的练习中,在某处击球,其飞行路线满足抛物线y=-$\frac{1}{5}$x2+$\frac{8}{5}$x,其中y(m)是球飞行的高度,x(m)是球飞行的水平距离.