题目内容
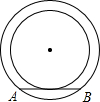 如图,两个同心圆的半径分别为4cm和5cm,大圆的一条弦AB与小圆相切,则弦AB的长为
如图,两个同心圆的半径分别为4cm和5cm,大圆的一条弦AB与小圆相切,则弦AB的长为考点:切线的性质,勾股定理,垂径定理
专题:计算题
分析:作OC⊥AB于C,连结OA,如图,根据切线的性质,由弦AB与小圆相切得到OC等于小圆的半径4cm,再利用勾股定理计算出AC=3,然后根据垂径定理得到AC=BC,则AB=2AC=6cm.
解答:解:作OC⊥AB于C,连结OA,如图,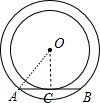
∵弦AB与小圆相切,
∴OC=4cm,
在Rt△OAC中,∵OA=5,OC=4,
∴AC=
=3,
∵OC⊥AB,
∴AC=BC,
∴AB=2AC=6cm.
故答案为6.

∵弦AB与小圆相切,
∴OC=4cm,
在Rt△OAC中,∵OA=5,OC=4,
∴AC=
| OA2-OC2 |
∵OC⊥AB,
∴AC=BC,
∴AB=2AC=6cm.
故答案为6.
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了垂径定理和勾股定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在钟面上,10点30分时的时针和分针所成的角的度数为( )
| A、100° | B、110° |
| C、120° | D、135° |
某小组为了解本校学生的视力情况,分别作了四种抽样调查的方案,你认为方案比较合理的是( )
| A、调查邻近学校200名学生的视力情况 |
| B、随机调查本校九年级50名学生的视力情况 |
| C、从每年级随机调查2个学生的视力情况 |
| D、随机调查本校各年级10%的学生视力情况 |

 如图,Rt△ABC中,CD是斜边AB上的高.求证:△ACD∽△ABC.
如图,Rt△ABC中,CD是斜边AB上的高.求证:△ACD∽△ABC. 如图,某单行遂道的截面是一个半径为3.6米的半圆形,一辆高为2.4米、宽3米的卡车能否通过遂道,请你判断并说明理由.
如图,某单行遂道的截面是一个半径为3.6米的半圆形,一辆高为2.4米、宽3米的卡车能否通过遂道,请你判断并说明理由. 如图,△ABC中,AD平分∠BAC,AE⊥BC于E,已知∠A=108°,∠C=2∠B,求∠DAE的度数.
如图,△ABC中,AD平分∠BAC,AE⊥BC于E,已知∠A=108°,∠C=2∠B,求∠DAE的度数.