题目内容
15. 把一副三角尺ABC与BDE按如图所示那样拼在一起,其中A、B、D三点在同一直线上,BM为∠CBE的平分线,BN为∠DBE的平分线,则∠MBN的度数是( )
把一副三角尺ABC与BDE按如图所示那样拼在一起,其中A、B、D三点在同一直线上,BM为∠CBE的平分线,BN为∠DBE的平分线,则∠MBN的度数是( )| A. | 60° | B. | 67.5° | C. | 75° | D. | 85° |
分析 由角平分线的定义可知∠EBN=$\frac{1}{2}∠EBD$=$\frac{1}{2}×45°$=22.5°,由平角的定义可知∠CBE=180°-∠ABC-∠DBE=180°-30°-45°=105°,再利用角平分线的定义可得∠EBM,可得结果.
解答 解:∵∠CBE=180°-∠ABC-∠DBE=180°-30°-45°=105°,BM为∠CBE的平分线,BN为∠DBE的平分线,
∴∠EBN=$\frac{1}{2}∠EBD$=$\frac{1}{2}×45°$=22.5°,$∠EBM=\frac{1}{2}∠CBE=\frac{1}{2}×105°$=52.5°,
∴∠MBN=∠MBE+∠EBN=52.5°+22.5°=75°,
故选C.
点评 本题主要考查了角平分线的定义,利用角平分线的定义计算角的度数是解答此题的关键.

练习册系列答案
相关题目
10. 如图,在正方形ABCD中,AB=2$\sqrt{2}$,连接AC,以点C为圆心、AC长为半径画弧,点E在BC的延长线上,则阴影部分的面积为( )
如图,在正方形ABCD中,AB=2$\sqrt{2}$,连接AC,以点C为圆心、AC长为半径画弧,点E在BC的延长线上,则阴影部分的面积为( )
 如图,在正方形ABCD中,AB=2$\sqrt{2}$,连接AC,以点C为圆心、AC长为半径画弧,点E在BC的延长线上,则阴影部分的面积为( )
如图,在正方形ABCD中,AB=2$\sqrt{2}$,连接AC,以点C为圆心、AC长为半径画弧,点E在BC的延长线上,则阴影部分的面积为( )| A. | 6π-4 | B. | 6π-8 | C. | 8π-4 | D. | 8π-8 |
7.要使分式$\frac{2x}{x+3}$有意义,则x的取值应满足( )
| A. | x=0 | B. | x≠0 | C. | x=-3 | D. | x≠-3 |
 如图,a∥b,∠1=∠2,∠3=40°,则∠4等于70度.
如图,a∥b,∠1=∠2,∠3=40°,则∠4等于70度. 如图,直线l1、l2、…l6是一组等距离的平行线,过直线l1上的点A作两条射线,分别与直线l3,l6相交于点B、E、C、F.若BC=2,则EF的长是( )
如图,直线l1、l2、…l6是一组等距离的平行线,过直线l1上的点A作两条射线,分别与直线l3,l6相交于点B、E、C、F.若BC=2,则EF的长是( )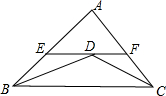 如图,△ABC中,BD平分∠ABC,CD平分∠ACB,过点D作EF∥BC,与AB、AC分别相交于E、F.若已知AB=9,AC=7,BC=8,求△AEF的周长.
如图,△ABC中,BD平分∠ABC,CD平分∠ACB,过点D作EF∥BC,与AB、AC分别相交于E、F.若已知AB=9,AC=7,BC=8,求△AEF的周长. 已知二次函数y=-x2+bx+c经过点(1,5),(3,1).
已知二次函数y=-x2+bx+c经过点(1,5),(3,1).