题目内容
 如图,已知AB是⊙O的直径,弦CD垂直平分半径OB,垂足为E,∠CDB=30°,OE=1,求图中阴影部分的面积.
如图,已知AB是⊙O的直径,弦CD垂直平分半径OB,垂足为E,∠CDB=30°,OE=1,求图中阴影部分的面积.考点:垂径定理,扇形面积的计算
专题:
分析:如图,作辅助线,证明S△OCE=S△ODE=S△BDE,进而证明S阴影=S扇形OBC;求出S扇形BOC=
=
,问题即可解决.
| 60π×22 |
| 360 |
| 2π |
| 3 |
解答: 解:如图,连接OD;
解:如图,连接OD;
∵弦CD垂直平分半径OB,
∴OE=BE,CE=DE,OB=2OE=2;
∴
OE•CE=
OE•DE=
BE•DE,
即S△OCE=S△ODE=S△BDE,
∴S阴影=S扇形OBC;
∵∠CDB=30°,
∴∠BOC=60°,
∴S扇形BOC=
=
,
即图中阴影部分的面积为
.
 解:如图,连接OD;
解:如图,连接OD;∵弦CD垂直平分半径OB,
∴OE=BE,CE=DE,OB=2OE=2;
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即S△OCE=S△ODE=S△BDE,
∴S阴影=S扇形OBC;
∵∠CDB=30°,
∴∠BOC=60°,
∴S扇形BOC=
| 60π×22 |
| 360 |
| 2π |
| 3 |
即图中阴影部分的面积为
| 2π |
| 3 |
点评:该题以圆为载体,以垂径定理、扇形面积公式的考查为核心构造而成;解题的关键是作辅助线,将求非规则图形的面积转化为求规则图形的面积.

练习册系列答案
相关题目
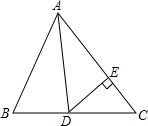 如图所示,在△ABC中,已知AD是角平分线,∠B=66°,∠C=54°.
如图所示,在△ABC中,已知AD是角平分线,∠B=66°,∠C=54°. 如图,已知⊙I内切于△ABC,切点分别分别为D、E、F,试说明,∠BIC=90°+
如图,已知⊙I内切于△ABC,切点分别分别为D、E、F,试说明,∠BIC=90°+