Question

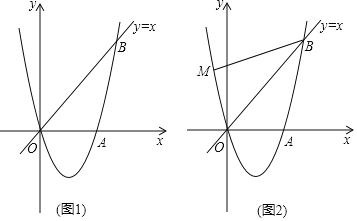
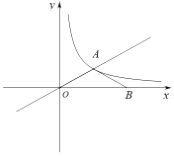
【题目】如图，在平面直角坐标系中，为坐标原点，正比例函数的图象与反比例函数的图象都经过点．点在轴上，且，反比例函数图象上有一点，且，则点坐标为____．

Answer 1

【答案】

【解析】

过点A作AD⊥OB于点D，过点C作CE⊥x轴于点E，先求出点A的坐标以及AB的长，设C(x，y)，再证ABD~BCE，CE=BE，得y=(x-6)，联立方程组，进而即可求解．

过点A作AD⊥OB于点D，过点C作CE⊥x轴于点E，

∵正比例函数的图象与反比例函数的图象都经过点．

∴，

∴D(3，0)，

∵，AD⊥OB，

∴OB=2OD=6，BD=OD=3，

∴B(6，0)，

∴AB==2，

设C(x，y)，

∵AD⊥OB，CE⊥x轴，

∴∠ADB=∠CEB=90°，∠DAB+∠ABD=90°，

∵∠ABC=90°，

∴∠CBE+∠ABD=90°，

∴∠DAB=∠CBE，

∴ABD~BCE，

∴，即，

∴CE=BE，

∴y=(x-6)，

∵点C在反比例函数上，

联立得方程组：，解得：或（舍去），

∴点C的坐标是：．

故答案是：．