题目内容
15.写出最简公分母:$\frac{1}{{m}^{2}+mn}$,$\frac{2}{{n}^{2}-{m}^{2}}$,$\frac{1}{{m}^{2}+{n}^{2}}$m(m2+n2)(n2-m2).分析 确定最简公分母的方法是:
(1)取各分母系数的最小公倍数;
(2)凡单独出现的字母连同它的指数作为最简公分母的一个因式;
(3)同底数幂取次数最高的,得到的因式的积就是最简公分母.
解答 解:$\frac{1}{{m}^{2}+mn}$,$\frac{2}{{n}^{2}-{m}^{2}}$,$\frac{1}{{m}^{2}+{n}^{2}}$ 的最简公分母为:m(m2+n2)(n2-m2),
故答案为:m(m2+n2)(n2-m2),
点评 本题考查了最简公分母,通分的关键是准确求出各个分式中分母的最简公分母,确定最简公分母的方法一定要掌握.

练习册系列答案
相关题目
 如图,在Rt△ABC中,∠C=90°,AB的垂直平分线交BC于点E,BC=4,AC=3,则△ACE的周长为7.
如图,在Rt△ABC中,∠C=90°,AB的垂直平分线交BC于点E,BC=4,AC=3,则△ACE的周长为7. 如图,BE=AD,AB=BC,BP为一条射线,AD⊥BP,CE⊥PB,若BD=6.求EC的长.
如图,BE=AD,AB=BC,BP为一条射线,AD⊥BP,CE⊥PB,若BD=6.求EC的长.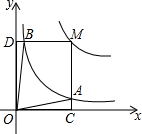 反比例函数y=$\frac{a}{x}$(a>0,a为常数)和y=$\frac{2}{x}$在第一象限内的图象如图所示,点M在y=$\frac{a}{x}$的图象上,MC⊥x轴于点C,交y=$\frac{2}{x}$的图象于点A;MD⊥y轴于点D,交y=$\frac{2}{x}$的图象于点B,当点M在y=$\frac{a}{x}$的图象上运动时,以下结论:
反比例函数y=$\frac{a}{x}$(a>0,a为常数)和y=$\frac{2}{x}$在第一象限内的图象如图所示,点M在y=$\frac{a}{x}$的图象上,MC⊥x轴于点C,交y=$\frac{2}{x}$的图象于点A;MD⊥y轴于点D,交y=$\frac{2}{x}$的图象于点B,当点M在y=$\frac{a}{x}$的图象上运动时,以下结论: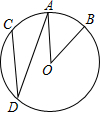 如图,点A,B,C,D分别在⊙O上,$\widehat{AB}$=$\widehat{AC}$,若∠AOB=40°,则∠ADC的大小是20度.
如图,点A,B,C,D分别在⊙O上,$\widehat{AB}$=$\widehat{AC}$,若∠AOB=40°,则∠ADC的大小是20度.