题目内容
4．
如图，在△ABC中，∠BAC=5∠ABC，∠C=2∠ABC，BD⊥AC，垂足为D．求证：∠CBD=45°．
分析 先根据∠BAC=5∠ABC，∠C=2∠ABC，设∠ABC=x，再根据∠ABC+∠BAC+∠ACB=180°，列出方程求解，最后根据三角形内角和定理，求得∠CBD的度数．
解答 解：∵∠BAC=5∠ABC，∠C=2∠ABC，
∴可设∠ABC=x，则∠BAC=5x，∠C=2x，
∵∠ABC+∠BAC+∠ACB=180°，
∴x+5x+2x=180°，
∴x=22.5°，
∴∠C=45°，
∵BD⊥AC，
∴Rt△BCD中，∠CBD=45°．
点评 本题主要考查了三角形内角和定理的运用，解题的关键是根据三角形内角和为180°，列出方程求解．
练习册系列答案
课课优能力培优100分系列答案
优百分课时互动系列答案
相关题目
12．
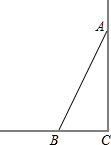如图，一根长为5m的竹竿AB斜靠在竖直的墙壁上，竹竿底端B离墙壁距离3m，则该竹竿的顶端A离地竖直高度为（ ）
如图，一根长为5m的竹竿AB斜靠在竖直的墙壁上，竹竿底端B离墙壁距离3m，则该竹竿的顶端A离地竖直高度为（ ）| A． | 2m | B． | 3m | C． | 4m | D． | $\sqrt{34}$m |
如图，在⊙O中，CD为直径，AB为弦，且CD平分AB于E，DE=2cm，AB=8cm．求：⊙O的半径．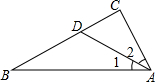
如图，∠C=90°，∠1=∠2，AB=15，CD=4，求△ABD的面积．