Question

4．如图，△ABC是直角三角形，∠ACB=90°．
（1）尺规作图：作⊙C，使它与AB相切于点D，与AC交于E．保留作图痕迹，不写作法，请标明字母．
（2）在你按（1）中要求所作的图中，若BC=3，∠A=30°，求$\widehat{DE}$的长．

Answer 1

分析 （1）过点C作CD⊥AB于点，然后以点C为圆心，CD为半径作图即可；
（2）利用切线的性质得∠ADC=90°，利用含30度的直角三角形三边的关系，在Rt△ACB中计算出AC=3$\sqrt{3}$，在Rt△ACD中计算出∠ACD=60°，CD=$\frac{1}{2}$AC=$\frac{3\sqrt{3}}{2}$，然后根据弧长公式计算$\widehat{DE}$的长．

解答 解：（1）如图，⊙C为所作；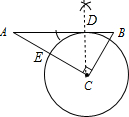

（2）∵⊙C与AB相切于点D，
∴CD⊥AB，
∴∠ADC=90°，
在Rt△ACB中，∵∠A=30°，
∴AC=$\sqrt{3}$BC=3$\sqrt{3}$，
在Rt△ACD中，∵∠A=30°，
∴∠ACD=60°，CD=$\frac{1}{2}$AC=$\frac{3\sqrt{3}}{2}$，
∴$\widehat{DE}$的长=$\frac{60•π•\frac{3\sqrt{3}}{2}}{180}$=$\frac{\sqrt{3}}{2}$π．

点评 本题考查了切线的性质：圆的切线垂直于经过切点的半径．也考查了基本作图和弧长公式．