题目内容
2.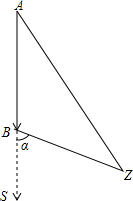 我渔政巡逻艇在A处测得距钓鱼岛Z的距离140海里,向南直行到B出测得距钓鱼岛Z的距离100海里,此时测得直行方向与钓鱼岛Z方向夹角为α,如图所示.求渔政巡逻艇行驶路程AB是多少海里?(sinα=$\frac{{\sqrt{3}}}{2}$,cosα=$\frac{1}{2}$,tanα=$\sqrt{3}$).
我渔政巡逻艇在A处测得距钓鱼岛Z的距离140海里,向南直行到B出测得距钓鱼岛Z的距离100海里,此时测得直行方向与钓鱼岛Z方向夹角为α,如图所示.求渔政巡逻艇行驶路程AB是多少海里?(sinα=$\frac{{\sqrt{3}}}{2}$,cosα=$\frac{1}{2}$,tanα=$\sqrt{3}$).
分析 作ZC⊥AB于点C,在直角△BCZ中利用三角函数求得BC和CZ,然后在直角△ACZ中利用勾股定理求得AC的长,则AB即可求解.
解答  解:作ZC⊥AB于点C.
解:作ZC⊥AB于点C.
∵在直角△BCZ中,sina=$\frac{CZ}{BZ}$=$\frac{\sqrt{3}}{2}$,cosa=$\frac{BC}{BZ}$,
∴CZ=$\frac{\sqrt{3}}{2}$BZ=50$\sqrt{3}$(海里),BC=$\frac{1}{2}$BZ=50(海里).
在直角△ACZ中,AC=$\sqrt{A{Z}^{2}-C{Z}^{2}}$=$\sqrt{14{0}^{2}-(50\sqrt{3})^{2}}$=110.
∴AB=AC-BC=110-50=60(海里).
答:渔政巡逻艇行驶路程AB是60海里.
点评 本题考查了三角函数以及勾股定理,正确记忆三角函数的定义是解决本题的关键.

练习册系列答案
相关题目
12. 如图,矩形ABCD中,对角线AC、BD相交于点O,则下列结论不正确的是( )
如图,矩形ABCD中,对角线AC、BD相交于点O,则下列结论不正确的是( )
 如图,矩形ABCD中,对角线AC、BD相交于点O,则下列结论不正确的是( )
如图,矩形ABCD中,对角线AC、BD相交于点O,则下列结论不正确的是( )| A. | AC⊥BD | B. | AC=BD | C. | BO=DO | D. | AO=CO |
13.为防治雾霾,保护环境,某市掀起“爱绿护绿”热潮,经过两年时间,绿地面积增加了21%,则这两年的绿地面积的平均增长率是( )
| A. | 10% | B. | 11.5% | C. | 12% | D. | 21% |
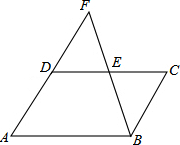 如图,点E是平行四边形ABCD的边CD的中点,AD、BE的延长线相交于点F,DF=3,DE=2,则平行四边形ABCD的周长为14.
如图,点E是平行四边形ABCD的边CD的中点,AD、BE的延长线相交于点F,DF=3,DE=2,则平行四边形ABCD的周长为14. 如图,在矩形ABCD中,AB=6,AD=10.
如图,在矩形ABCD中,AB=6,AD=10. 如图,在边长为4的正方形ABCD中,E、F分别是CD、AD上的点,且CE=DF,BE、CF交于点M.
如图,在边长为4的正方形ABCD中,E、F分别是CD、AD上的点,且CE=DF,BE、CF交于点M.