题目内容
10.某超市计划购进一批甲、乙两种玩具,已知3件甲种玩具的进价与2件乙种玩具的进价的和为142元,2件甲种玩具的进价与4件乙种玩具的进价的和为164元.(1)求每件甲、乙两种玩具的进价分别是多少?
(2)如果购进甲种玩具超过10件,超出部分可以享受7折优惠.超市决定在甲、乙两种玩具中选购其中一种,且数量超过10件,试帮助超市判断购进哪种玩具省钱.
分析 (1)设每件甲种玩具的进价是x元,每件乙种玩具的进价是y元,根据“3件甲种玩具的进价与2件乙种玩具的进价的和为142元,2件甲种玩具的进价与4件乙种玩具的进价的和为164元”列出方程组解决问题;
(2)设购进玩具z件(z>10),分别表示出甲种和乙种玩具消费,建立不等式解决问题.
解答 解:(1)设甲种玩具的进价是x元,乙种玩具的进价是y元,由题意得:
$\left\{\begin{array}{l}{3x+2y=142}\\{2x+4y=164}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=30}\\{y=26}\end{array}\right.$.
答:甲种玩具的进价是30元,乙种玩具的进价是26元;
(2)设购进玩具z件(z>10),则乙种玩具消费26z元,甲种玩具消费10×30+(z-10)×30×0.7元,
①当26z=10×30+(z-10)×30×0.7,
解得z=18.
所以当购进玩具正好18件,选择购其中一种即可;
②当26z>10×30+(z-10)×30×0.7,
解得z>18.
所以当购进玩具超过18件,选择购甲种玩具省钱;
③当26z<10×30+(z-10)×30×0.7,
解得z<18.
所以当购进玩具少于18件,多于10件,选择购乙种玩具省钱.
点评 此题主要考查二元一次方程组,一元一次不等式的运用,关键是理解题意,找出题目中的等量关系和不等关系,列出方程和不等式.

练习册系列答案
相关题目
20.去年国庆假期,天安门接待游客日平均为10.7万人,这个假期7天共接待的游客人数用科学记数法可表示为( )
| A. | 1.07×105人 | B. | 7.49×104人 | C. | 7.49×105人 | D. | 7.49×106人 |
15.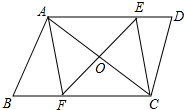 如图,平行四边形ABCD中,EF垂直平分AC,与边AD、BC分别相交于点E、F.则四边形AECF一定是( )
如图,平行四边形ABCD中,EF垂直平分AC,与边AD、BC分别相交于点E、F.则四边形AECF一定是( )
 如图,平行四边形ABCD中,EF垂直平分AC,与边AD、BC分别相交于点E、F.则四边形AECF一定是( )
如图,平行四边形ABCD中,EF垂直平分AC,与边AD、BC分别相交于点E、F.则四边形AECF一定是( )| A. | 正方形 | B. | 矩形 | C. | 菱形 | D. | 不能确定 |
 如图,平行四边形ABCD是对角线互相垂直的四边形,请你添加一个适当的条
如图,平行四边形ABCD是对角线互相垂直的四边形,请你添加一个适当的条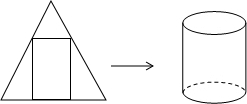 如图,在一个边长为4的等边三角形纸片中,截出一个面积最大的矩形,并用该矩形围成一个圆柱形无底纸筒,则纸筒的高为2或$\sqrt{3}$.
如图,在一个边长为4的等边三角形纸片中,截出一个面积最大的矩形,并用该矩形围成一个圆柱形无底纸筒,则纸筒的高为2或$\sqrt{3}$. 如图,直线a∥b,点B在直线b上,且AB⊥BC,∠2=35°,则∠1=55°.
如图,直线a∥b,点B在直线b上,且AB⊥BC,∠2=35°,则∠1=55°.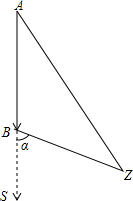 我渔政巡逻艇在A处测得距钓鱼岛Z的距离140海里,向南直行到B出测得距钓鱼岛Z的距离100海里,此时测得直行方向与钓鱼岛Z方向夹角为α,如图所示.求渔政巡逻艇行驶路程AB是多少海里?(sinα=$\frac{{\sqrt{3}}}{2}$,cosα=$\frac{1}{2}$,tanα=$\sqrt{3}$).
我渔政巡逻艇在A处测得距钓鱼岛Z的距离140海里,向南直行到B出测得距钓鱼岛Z的距离100海里,此时测得直行方向与钓鱼岛Z方向夹角为α,如图所示.求渔政巡逻艇行驶路程AB是多少海里?(sinα=$\frac{{\sqrt{3}}}{2}$,cosα=$\frac{1}{2}$,tanα=$\sqrt{3}$).