题目内容
17.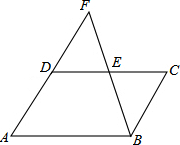 如图,点E是平行四边形ABCD的边CD的中点,AD、BE的延长线相交于点F,DF=3,DE=2,则平行四边形ABCD的周长为14.
如图,点E是平行四边形ABCD的边CD的中点,AD、BE的延长线相交于点F,DF=3,DE=2,则平行四边形ABCD的周长为14.
分析 由平行四边形的性质得出AB=CD,AD=BC,AD∥BC,证出∠CBE=∠F,由AAS证明△BCE≌△FDE,得出BC=DF=3,即可求出平行四边形ABCD的周长.
解答 解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,AD∥BC,
∴∠CBE=∠F,
∵E是CD的中点,
∴CE=DE=2,CD=2DE=4,
在△BCE和△FDE中,$\left\{\begin{array}{l}{∠CBE=∠F}&{\;}\\{∠BEC=∠FED}&{\;}\\{CE=DE}&{\;}\end{array}\right.$,
∴△BCE≌△FDE(AAS),
∴BC=DF=3,
∴平行四边形ABCD的周长=2(BC+CD)=2(3+4)=14;
故答案为:14.
点评 本题考查了平行四边形的性质、全等三角形的判定与性质、平行四边形周长的计算;熟练掌握平行四边形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
8.我国南海海域面积为3800000km2,用科学记数法表示正确的是( )
| A. | 3.8×105km2 | B. | 3.8×106km2 | C. | 3.8×107km2 | D. | 3.8×108km2 |
12.不等式-3x<6的解集为( )
| A. | x<-2 | B. | x>-2 | C. | x<2 | D. | x>2 |
2.已知3x=4y(x≠4),则下列各式不成立的是( )
| A. | $\frac{x}{3}$=$\frac{y}{4}$ | B. | $\frac{x+4}{4}$=$\frac{y+3}{3}$ | C. | $\frac{x+y}{4+3}$=$\frac{x}{4}$ | D. | $\frac{4-x}{x}$=$\frac{3-y}{y}$ |
 如图,直线a∥b,点B在直线b上,且AB⊥BC,∠2=35°,则∠1=55°.
如图,直线a∥b,点B在直线b上,且AB⊥BC,∠2=35°,则∠1=55°.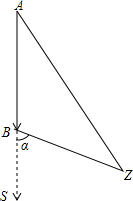 我渔政巡逻艇在A处测得距钓鱼岛Z的距离140海里,向南直行到B出测得距钓鱼岛Z的距离100海里,此时测得直行方向与钓鱼岛Z方向夹角为α,如图所示.求渔政巡逻艇行驶路程AB是多少海里?(sinα=$\frac{{\sqrt{3}}}{2}$,cosα=$\frac{1}{2}$,tanα=$\sqrt{3}$).
我渔政巡逻艇在A处测得距钓鱼岛Z的距离140海里,向南直行到B出测得距钓鱼岛Z的距离100海里,此时测得直行方向与钓鱼岛Z方向夹角为α,如图所示.求渔政巡逻艇行驶路程AB是多少海里?(sinα=$\frac{{\sqrt{3}}}{2}$,cosα=$\frac{1}{2}$,tanα=$\sqrt{3}$).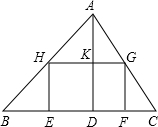 如图,在△ABC中,AD是BC边上的高,BC=12,AD=8,矩形EFGH的边EF与BC重合,点G、H分别在AC、AB上运动.
如图,在△ABC中,AD是BC边上的高,BC=12,AD=8,矩形EFGH的边EF与BC重合,点G、H分别在AC、AB上运动.