题目内容
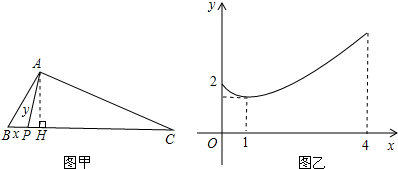
20. 已知:DE∥BC,求证:DG•BF=GE•FC.
已知:DE∥BC,求证:DG•BF=GE•FC.
分析 由DE∥BC,可证明△DGH∽△CFH,△GEH∽△FBH,△DEH∽△CBH,再根据相似三角形的性质:对应边的比值相等即可证明DG•BF=GE•FC.
解答 证明:∵DE∥BC,
∴△DGH∽△CFH,△GEH∽△FBH,△DEH∽△CBH,
∴$\frac{DG}{FC}=\frac{DH}{CH}$,$\frac{GE}{BF}=\frac{EH}{BH}$,$\frac{DH}{CH}=\frac{EH}{BH}$,
∴$\frac{DG}{FC}=\frac{GE}{BF}$,
即DG•BF=GE•FC.
点评 本题考查了相似三角形的判定和性质,解题的关键是通过证明△DEH∽△CBH,得到$\frac{DH}{CH}=\frac{EH}{BH}$,即中间比值.

练习册系列答案
相关题目
14.某年级有四个班,人数分别为:一班25人,二班22人,三班27人,四班26人.在一次考试中,四个班的班级平均分依次为81分,75分,89分,78分,则这次考试的年级平均分为( )
| A. | 79.25分 | B. | 80.75分 | C. | 81.06分 | D. | 82.53分 |
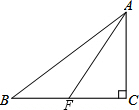 如图,在△ABC中,∠C=90°,AC=6,AB=10,F是BC边上一点.
如图,在△ABC中,∠C=90°,AC=6,AB=10,F是BC边上一点.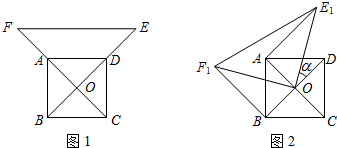
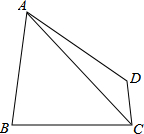 如图,在四边形ABCD中,AD=AB=BC,连接AC,且∠ACD=30°,tan∠BAC=$\frac{{2\sqrt{3}}}{3}$,CD=3,则AC=6$\sqrt{3}$.
如图,在四边形ABCD中,AD=AB=BC,连接AC,且∠ACD=30°,tan∠BAC=$\frac{{2\sqrt{3}}}{3}$,CD=3,则AC=6$\sqrt{3}$.