题目内容
如图，在矩形ABCD中，点E为AB的中点，点F为AD上一点，EF交AC于点G，AF=4cm，DF=8cm，AG=5cm，则AC的长为（ ）| A、25cm | B、15cm |
| C、12.5cm | D、7.5cm |
考点：相似三角形的判定与性质,矩形的性质
专题：
分析：延长FG交CB的延长线于点H．根据平行四边形的性质，得BC=AD=12cm，BC∥AD．根据AAS可以证明△AFE≌△BHE，则BH=AF=4cm，再根据BC∥AD，求得CG的长，从而求得AC的长．
解答：解：
∵四边形ABCD是矩形，
∴BC=AD=12cm，BC∥AD．
∴∠EAF=∠EBH，∠AFE=∠BHE，
在△AFE与△BHE中
∴△AFE≌△BHE（AAS）
∴BH=AF=4cm．
∵BC∥AD，
∴
=
，
即
=
则CG=20，
则AC=AG+CG=25（cm）．
故选A．
∵四边形ABCD是矩形，∴BC=AD=12cm，BC∥AD．
∴∠EAF=∠EBH，∠AFE=∠BHE，
在△AFE与△BHE中
|
∴△AFE≌△BHE（AAS）
∴BH=AF=4cm．
∵BC∥AD，
∴
| AG |
| CG |
| AF |
| HC |
即
| 5 |
| CG |
| 4 |
| 16 |
则CG=20，
则AC=AG+CG=25（cm）．
故选A．
点评：此题综合考查了矩形的性质、全等三角形的判定及性质、平行线分线段成比例定理．此题中要能够巧妙构造辅助线．
练习册系列答案
名校课堂系列答案
相关题目
下列等式成立的是（ ）
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、-
|
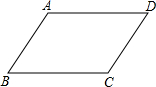如图，已知在平行四边形ABCD中，AD=4cm，AB=3cm，则平行四边形ABCD的周长等于（ ）| A、16cm | B、14cm |
| C、12cm | D、10cm |
已知三角形内的一个点到它的三边距离相等，那么这个点是（ ）
| A、三角形的外心 |
| B、三角形的重心 |
| C、三角形的内心 |
| D、三角形的垂心 |
下列各式：
①（-7）+（-7）=0；②（-3）2=-9；③（-2）3=-6；④-33=-27；⑤
=
．
其中运算正确的有（ ）
①（-7）+（-7）=0；②（-3）2=-9；③（-2）3=-6；④-33=-27；⑤
| 22 |
| 3 |
| 4 |
| 9 |
其中运算正确的有（ ）
| A、0个 | B、1个 | C、2个 | D、3个 |
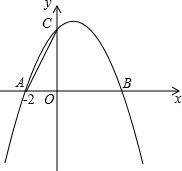如图，已知抛物线y=ax2+bx+4与x轴交于A（-2，0）、B两点，与y轴交于C点，其对称轴为直线x=1．
如图，已知抛物线y=x2+bx+c与x轴交于点A、B，且A（1，0），与y轴交于点C，对称轴为直线x=2．