题目内容
观察下列等式:
第1个等式:a1= =
= ×(1-
×(1- );
);
第2个等式:a2=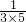 =
= ×(
×( -
- );
);
第3个等式:a3=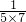 =
= ×(
×( -
- );
);
第4个等式:a4= =
= ×(
×( -
- );
);
…
请解答下列问题:
(1)按以上规律列出第5个等式:a5=______=______;
(2)求a1+a2+a3+a4+…+a100的值为______.
解:(1)第1个等式:a1= =
= ×(1-
×(1- );
);
第2个等式:a2=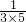 =
= ×(
×( -
- );
);
第3个等式:a3=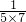 =
= ×(
×( -
- );
);
第4个等式:a4= =
= ×(
×( -
- );
);
…
则第5个等式:a5= =
= ×(
×( -
- );
);
故答案为: ,
, ×(
×( -
- );
);
(2)a1+a2+a3+a4+…+a100
= ×(1-
×(1- )+
)+ ×(
×( -
- )+…+
)+…+ ×(
×( -
- ),
),
= ×(1-
×(1- +
+ -
- +…+
+…+ -
- ),
),
= ×(1-
×(1- ),
),
= .
.
故答案为: .
.
分析:(1)观察知,找第一个等号后面的式子规律是关键:分子不变,为1;分母是两个连续奇数的乘积,它们与式子序号之间的关系为:序号的2倍减1和序号的2倍加1.
(2)运用(1)中变化规律计算得出即可.
点评:此题考查了数字的规律及运用规律计算.寻找规律大致可分为2个步骤:不变的和变化的;变化的部分与序号的关系.
 =
= ×(1-
×(1- );
);第2个等式:a2=
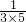 =
= ×(
×( -
- );
);第3个等式:a3=
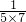 =
= ×(
×( -
- );
);第4个等式:a4=
 =
= ×(
×( -
- );
);…
则第5个等式:a5=
 =
= ×(
×( -
- );
);故答案为:
 ,
, ×(
×( -
- );
);(2)a1+a2+a3+a4+…+a100
=
 ×(1-
×(1- )+
)+ ×(
×( -
- )+…+
)+…+ ×(
×( -
- ),
),=
 ×(1-
×(1- +
+ -
- +…+
+…+ -
- ),
),=
 ×(1-
×(1- ),
),=
 .
.故答案为:
 .
.分析:(1)观察知,找第一个等号后面的式子规律是关键:分子不变,为1;分母是两个连续奇数的乘积,它们与式子序号之间的关系为:序号的2倍减1和序号的2倍加1.
(2)运用(1)中变化规律计算得出即可.
点评:此题考查了数字的规律及运用规律计算.寻找规律大致可分为2个步骤:不变的和变化的;变化的部分与序号的关系.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
 ;
; ;
; ;
; ;
; = = ;
= = ; = = (n为正整数);
= = (n为正整数); 的值.
的值. ;
; ;
; ;
; ;
;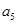 =
= ;
=
= ;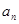 =
= (n为正整数);
=
= (n为正整数);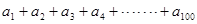 的值.
的值.