题目内容
15、观察下列等式:
第1个等式:42-12=3×5;
第2个等式:52-22=3×7;
第3个等式:62-32=3×9;
第4个等式:72-42=3×11;
…
则第n(n是正整数)个等式为
第1个等式:42-12=3×5;
第2个等式:52-22=3×7;
第3个等式:62-32=3×9;
第4个等式:72-42=3×11;
…
则第n(n是正整数)个等式为
(n+3)2-n2=3(2n+3)
.分析:观察上面的等式,左边是平方差公式的形式,右边是两个数积的形式,即(n+3)2-n2=3(2n+3).
解答:解:等式左边是平方差公式,即(n+3)2-n2=3(2n+3),
故答案为(n+3)2-n2=3(2n+3).
故答案为(n+3)2-n2=3(2n+3).
点评:通过观察,分析、归纳并发现其中的规律,并应用发现的规律解决问题是应该具备的基本能力.本题的关键规律为等号前面平方差公式,可以表示为(n+3)2-n2,等号右边表示的是两个数的积,表示成3(2n+3).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ;
; ;
; ;
; ;
; = = ;
= = ; = = (n为正整数);
= = (n为正整数); 的值.
的值.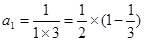 ;
; ;
;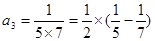 ;
; ;
;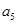 =
= ;
=
= ;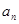 =
= (n为正整数);
=
= (n为正整数); 的值.
的值.