题目内容
8.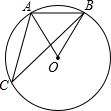 如图,点A,B,C是⊙O上的点,OA=AB,则∠C的度数为30°.
如图,点A,B,C是⊙O上的点,OA=AB,则∠C的度数为30°.
分析 由OA=AB,OA=OB,可得△OAB是等边三角形,即可得∠AOB=60°,又由在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半,即可求得∠C的度数.
解答 解:∵OA=AB,OA=OB,
∴OA=OB=AB,
即△OAB是等边三角形,
∴∠AOB=60°,
∴∠C=$\frac{1}{2}$∠AOB=30°.
故答案为30°.
点评 此题考查了圆周角定理与等边三角形的判定与性质.此题比较简单,注意掌握在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半定理的应用.

练习册系列答案
相关题目
18. 如图,AB是⊙O的直径,点A是弧CD的中点,若∠B=25°,则∠AOC=( )
如图,AB是⊙O的直径,点A是弧CD的中点,若∠B=25°,则∠AOC=( )
 如图,AB是⊙O的直径,点A是弧CD的中点,若∠B=25°,则∠AOC=( )
如图,AB是⊙O的直径,点A是弧CD的中点,若∠B=25°,则∠AOC=( )| A. | 25° | B. | 30° | C. | 40° | D. | 50° |
19. 如图,图中∠α的度数等于( )
如图,图中∠α的度数等于( )
 如图,图中∠α的度数等于( )
如图,图中∠α的度数等于( )| A. | 135° | B. | 125° | C. | 115° | D. | 105° |
20.下列各数中,绝对值最大的数是( )
| A. | 5 | B. | -3 | C. | 0 | D. | -2 |
17.张三和李四两人加工同一种零件,每小时张三比李四多加工5个零件,张三加工120个这种零件与李四加工100个这种零件所用时间相等,求张三和李四每小时各加工多少个这种零件?若设张三每小时经过这种零件x个,则下面列出的方程正确的是( )
| A. | $\frac{120}{x-5}$=$\frac{100}{x}$ | B. | $\frac{120}{x}$=$\frac{100}{x-5}$ | C. | $\frac{120}{x+5}$=$\frac{100}{x}$ | D. | $\frac{120}{x}$=$\frac{100}{x+5}$ |
 如图,已知点A1,A2,…,An均在直线y=x-1上,点B1,B2,…,Bn均在双曲线y=-$\frac{1}{x}$上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=-1,则a2015=2.
如图,已知点A1,A2,…,An均在直线y=x-1上,点B1,B2,…,Bn均在双曲线y=-$\frac{1}{x}$上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=-1,则a2015=2.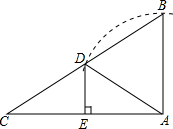 如图,在Rt△ABC中,∠C=30°,以直角顶点A为圆心,AB长为半径画弧交BC于点D,过D作DE⊥AC于点E.若DE=a,则△ABC的周长用含a的代数式表示为(6+2$\sqrt{3}$)a.
如图,在Rt△ABC中,∠C=30°,以直角顶点A为圆心,AB长为半径画弧交BC于点D,过D作DE⊥AC于点E.若DE=a,则△ABC的周长用含a的代数式表示为(6+2$\sqrt{3}$)a.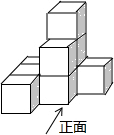 如图是由多个完全相同的小正方体组成的几何体,其左视图是( )
如图是由多个完全相同的小正方体组成的几何体,其左视图是( )