题目内容
8.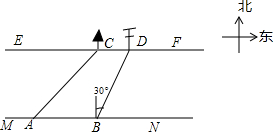 在综合实践课上,小聪所在小组要测量一条河的宽度,如图,河岸EF∥MN,小聪在河岸MN上点A处测得河对岸小树C位于东北方向,然后沿河岸走了30米,到达B处,测得河对岸电线杆D位于北偏东30°方向,此时,其他同学测得CD=10米.请根据这些数据求出河的宽度.(结果保留根号)
在综合实践课上,小聪所在小组要测量一条河的宽度,如图,河岸EF∥MN,小聪在河岸MN上点A处测得河对岸小树C位于东北方向,然后沿河岸走了30米,到达B处,测得河对岸电线杆D位于北偏东30°方向,此时,其他同学测得CD=10米.请根据这些数据求出河的宽度.(结果保留根号)
分析 如图作BH⊥EF,CK⊥MN,垂足分别为H、K,则四边形BHCK是矩形,设CK=HB=x,根据tan30°=$\frac{HD}{BH}$列出方程即可解决问题.
解答 解:如图作BH⊥EF,CK⊥MN,垂足分别为H、K,则四边形BHCK是矩形,
设CK=HB=x,
∵∠CKA=90°,∠CAK=45°,
∴∠CAK=∠ACK=45°,
∴AK=CK=x,BK=HC=AK-AB=x-30,
∴HD=x-30+10=x-20,
在RT△BHD中,∵∠BHD=90°,∠HBD=30°,
∴tan30°=$\frac{HD}{BH}$,
∴$\frac{\sqrt{3}}{3}$=$\frac{x-20}{x}$,
解得x=30+10$\sqrt{3}$.
∴河的宽度为(30+10$\sqrt{3}$)米.
点评 本题考查解直角三角形的应用、方向角、三角函数等知识,解题的关键是添加辅助线构造直角三角形,学会利用三角函数的定义,列出方程解决问题,属于中考常考题型.

练习册系列答案
相关题目
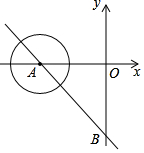 如图,在直角坐标系中直线AB分别交x轴,y轴与A(-6,0)、B(0,-8)两点,现有一半径为1的动圆,圆心由A点,沿着AB方向以每秒1个单位的速度做平移运动,则经过几秒后动圆与坐标轴相切.
如图,在直角坐标系中直线AB分别交x轴,y轴与A(-6,0)、B(0,-8)两点,现有一半径为1的动圆,圆心由A点,沿着AB方向以每秒1个单位的速度做平移运动,则经过几秒后动圆与坐标轴相切. 如图,在平面直角坐标系中,O为坐标原点,点N的坐标为(20,0),点M在第一象限内,且OM=10,sin∠MON=$\frac{3}{5}$.求:
如图,在平面直角坐标系中,O为坐标原点,点N的坐标为(20,0),点M在第一象限内,且OM=10,sin∠MON=$\frac{3}{5}$.求: