题目内容
13. 如图,D是△ABC的斜边BC上一点,DE⊥AB,DF⊥AC,EF是垂足,四边形AEDF的面积为y,BD为x.y与x的函数关系图象正确的是( )
如图,D是△ABC的斜边BC上一点,DE⊥AB,DF⊥AC,EF是垂足,四边形AEDF的面积为y,BD为x.y与x的函数关系图象正确的是( )| A. |  | B. |  | C. |  | D. |  |
分析 设BC=a,AB=c,AC=b,先证明△BDE∽△BCA,录用相似比可表示出DE=$\frac{b}{a}$x,利用同样方法得到DF=$\frac{c}{a}$(a-x),则根据矩形的面积公式得到y=-$\frac{bc}{{a}^{2}}$x2+$\frac{bc}{a}$x(0<x<a),于是得到y与x的函数图象为开口向下的抛物线,由此特征可对各选项进行判断.
解答 解:设BC=a,AB=c,AC=b,
∵DE⊥AB,
∴∠DEB=90°,
而∠DBE=∠CBA,
∴△BDE∽△BCA,
∴DE:CA=BD:BC,
∴DE=$\frac{b}{a}$x,
同理可得DF=$\frac{c}{a}$(a-x),
∴y=$\frac{b}{a}$x•$\frac{c}{a}$(a-x)=-$\frac{bc}{{a}^{2}}$x2+$\frac{bc}{a}$x(0<x<a).
故选B.
点评 本题考查了动点问题的函数图象:函数图象是典型的数形结合,图象应用信息广泛,通过看图获取信息,不仅可以解决生活中的实际问题,还可以提高分析问题、解决问题的能力.解决本题的关键是利用相似比用x表示出DE和DF.

练习册系列答案
相关题目
 如图,△ABC中,点P、Q、R分别在AB、BC、AC上,且PB=QC,QB=RC,点Q在PR的垂直平分线上,求证:∠B=∠C.
如图,△ABC中,点P、Q、R分别在AB、BC、AC上,且PB=QC,QB=RC,点Q在PR的垂直平分线上,求证:∠B=∠C. 如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:
如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题: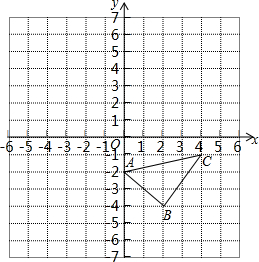 如图,在平面直角坐标系中,△ABC的三个顶点均在格点上.
如图,在平面直角坐标系中,△ABC的三个顶点均在格点上. 如图,P是⊙O外一动点,PA、PB、CD是⊙O的三条切线,C、D分别在PA、PB上,连接OC、OD.设∠P为x°,∠COD为y°,则y随x的函数关系图象为( )
如图,P是⊙O外一动点,PA、PB、CD是⊙O的三条切线,C、D分别在PA、PB上,连接OC、OD.设∠P为x°,∠COD为y°,则y随x的函数关系图象为( )



 某次火灾事故中,消防员架起一架AB=25米长的云梯.如图斜靠在一面墙上,梯子底端B离墙7米.
某次火灾事故中,消防员架起一架AB=25米长的云梯.如图斜靠在一面墙上,梯子底端B离墙7米. 如图,直线y=-2x+7与x轴、y轴分别相交于点C、B,与直线y=$\frac{3}{2}$x相交于点A.
如图,直线y=-2x+7与x轴、y轴分别相交于点C、B,与直线y=$\frac{3}{2}$x相交于点A.