题目内容
18．
如图，P是⊙O外一动点，PA、PB、CD是⊙O的三条切线，C、D分别在PA、PB上，连接OC、OD．设∠P为x°，∠COD为y°，则y随x的函数关系图象为（ ）| A． |  | B． |  | C． |  | D． |  |
分析 设CD与⊙O相切于点E，连结OA、OB、OE，如图，根据切线长定理得CA=CE，DE=DB，根据切线的性质得OA⊥PA，OB⊥PB，OE⊥CD，则利用角平分线定理的逆定理可判断OC平分∠AOE，OD平分∠BOE，则∠1=∠2，∠3=∠4，所以∠COD=$\frac{1}{2}$∠AOB，接着利用四边形内角和得到∠AOB=180°-∠P=180°-x°，所以y=90°-$\frac{1}{2}$x（0＜x＜180°），然后利用此解析式对各选项进行判断即可．
解答 解：设CD与⊙O相切于点E，连结OA、OB、OE，如图，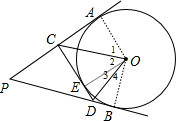
∵PA、PB、CD是⊙O的三条切线，
∵CA=CE，DE=DB，OA⊥PA，OB⊥PB，OE⊥CD，
∴OC平分∠AOE，OD平分∠BOE，
∴∠1=∠2，∠3=∠4，
∴∠COD=∠2+∠3=$\frac{1}{2}$∠AOB，
∵∠AOB=180°-∠P=180°-x°，
∴y=90°-$\frac{1}{2}$x（0＜x＜180°）．
故选B．
点评 本题考查了动点问题的函数图象：函数图象是典型的数形结合，图象应用信息广泛，通过看图获取信息，不仅可以解决生活中的实际问题，还可以提高分析问题、解决问题的能力．解决本题的关键是切线的性质的运用．
练习册系列答案
口算能手系列答案
相关题目
如图，在△ABC中，AD是∠BAC的平分线，交BC于点D，若AC=AB+BD，∠C=30°，求∠B的度数．
如图，在△ABD中，AB=6，AD=BD=5．点P以每秒1个单位长度的速度，由点A出发，沿边AB向点B运动，且满足∠DPC=∠A．
如图，D是△ABC的斜边BC上一点，DE⊥AB，DF⊥AC，EF是垂足，四边形AEDF的面积为y，BD为x．y与x的函数关系图象正确的是（ ）
3．
如图，在Rt△PQR中，∠PRQ=90°，RP=RQ，边RP在数轴上．点Q表示的数为1，点R表示的数为3，以Q为圆心，QP为半径画弧交数轴负半轴于点P1，则P1表示的是（ ）
如图，在Rt△PQR中，∠PRQ=90°，RP=RQ，边RP在数轴上．点Q表示的数为1，点R表示的数为3，以Q为圆心，QP为半径画弧交数轴负半轴于点P1，则P1表示的是（ ）| A． | -2 | B． | -2$\sqrt{2}$ | C． | 1-2$\sqrt{2}$ | D． | 2$\sqrt{2}$-1 |
10．如果给定数组中每一个数都加上同一个非零常数，则数据的（ ）
| A． | 平均数不变，方差不变 | B． | 平均数改变，方差改变 | ||
| C． | 平均数改变，方差不变 | D． | 平均数不变，方差改变 |
如图，在灯塔O处观测到轮船A位于北偏西54°的方向，同时轮船B在南偏东15°的方向，那么∠AOB=141°．
8．某公司准备投资开发A、B两种新产品，信息部通过调研得到两条信息：
信息一：如果投资A种产品，所获利润yA（万元）与投资金额x（万元）之间满足正比例函数关系：yA=kx；
信息二：如果投资B种产品，所获利润yB（万元）与投资金额x（万元）之间满足二次函数关系：yB=ax2+bx
根据公司信息部报告，yA、yB（万元）与投资金额x（万元）的部分对应值如下表所示：
（1）填空：yA=0.8x；yB=-0.1x2+2.4x；
（2）如果公司准备投资20万元同时开发A、B两种新产品，设公司所获得的总利润为W（万元），B种产品的投资金额为x（万元），试求出W与x之间的函数关系式；
（3）请你设计一个在（2）中公司能获得最大总利润的投资方案．
信息一：如果投资A种产品，所获利润yA（万元）与投资金额x（万元）之间满足正比例函数关系：yA=kx；
信息二：如果投资B种产品，所获利润yB（万元）与投资金额x（万元）之间满足二次函数关系：yB=ax2+bx
根据公司信息部报告，yA、yB（万元）与投资金额x（万元）的部分对应值如下表所示：
| X（万元） | 1 | 2 |
| yA（万元） | 0.8 | 1.6 |
| yB（万元） | 2.3 | 4.4 |
（2）如果公司准备投资20万元同时开发A、B两种新产品，设公司所获得的总利润为W（万元），B种产品的投资金额为x（万元），试求出W与x之间的函数关系式；
（3）请你设计一个在（2）中公司能获得最大总利润的投资方案．