题目内容
如图,在矩形ABCD中,E,F分别是边AB,CD的中点,连接AF,CE .
(1)求证:△BEC≌△DFA.
(2)求证:四边形AECF是平行四边形.

【证明 】(1)∵四边形ABCD是矩形,
】(1)∵四边形ABCD是矩形,
∴AB=CD,AD=BC.
又∵E,F分别是边AB,CD的中点,
∴BE=DF,
∵在△BEC和△DFA中,
 ∴△BEC≌△DFA(SAS).
∴△BEC≌△DFA(SAS).
(2)由(1)得,CE=AF,又CF=AE,
故可得四边形AECF是平行四边形.

练习册系列答案
相关题目
某公司有10名销售业务员,去年每人完成的销售额情况如表:
| 售额(万元) | 3 | 4 | 5 | 6 | 7 | 8 | 10 |
| 销售人数 | 1 | 3 | 2 | 1 | 1 | 1 | 1 |
问题:(1)求 10名销售员销售额的平均数、中位数和众数.(单位:万元)
10名销售员销售额的平均数、中位数和众数.(单位:万元)
(2 )为了调动员工积极性,公司准备采取超额有奖措施,请问把标准定为多少万元时最合适?
)为了调动员工积极性,公司准备采取超额有奖措施,请问把标准定为多少万元时最合适?
 ∥
∥ ,
, 是截线,若∠1=
是截线,若∠1= ,∠5=
,∠5= .求∠2、∠3、∠4各是多少度?为什么?
.求∠2、∠3、∠4各是多少度?为什么?
 那么这块地毯需要花 元.
那么这块地毯需要花 元.

 0°,则矩形ABCD的面积是( )
0°,则矩形ABCD的面积是( )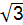 D.16
D.16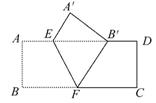
 C,AB于点D,F,BE⊥DF交DF的延长线于点E,已知∠A=30°,BC=2,AF=BF,则四边形BCDE的面积是( )
C,AB于点D,F,BE⊥DF交DF的延长线于点E,已知∠A=30°,BC=2,AF=BF,则四边形BCDE的面积是( )
 B.
B. D.∠ACB=60°
D.∠ACB=60°
