题目内容
15. 在平行四边形ABCD中,AE⊥BD于E,CF⊥BD于F,G,H分别为AD,BC的中点,求证:EF和GH互相平分.
在平行四边形ABCD中,AE⊥BD于E,CF⊥BD于F,G,H分别为AD,BC的中点,求证:EF和GH互相平分.
分析 首先连接BG、DH,由在平行四边形ABCD中,AE⊥BD于E,CF⊥BD于F,利用AAS证明△ABE≌△CDF,得出BE=DF,证明四边形BHDG是平行四边形,得出对角线互相平分OG=OH,OB=OD,求出OE=OF,结论得出结论.
解答 证明:连接BG、DH,如图所示: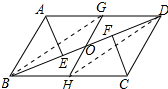
∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,AB∥CD,
∴∠ABE=∠CDF,
∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°,
在△ABE和△CDF中,
$\left\{\begin{array}{l}{∠ABE=∠CDF}\\{∠AEB=∠CFD}\\{AB=CD}\end{array}\right.$,
∴△ABE≌△CDF(AAS),
∴BE=DF,
∵G、H分别为AD、BC的中点,
∴DG=BH,
∴四边形BHDG是平行四边形,
∴OG=OH,OB=OD,
∴OB-BE=OD-DF,
∴OE=OF,
即EF、GH互相平分.
点评 本题考查了平行四边形的判定与性质以及全等三角形的判定与性质.注意准确作出辅助线是解此题的关键.

练习册系列答案
相关题目
7.二次根式$\sqrt{3x-1}$中字母x可以取的数是( )
| A. | 0 | B. | 2 | C. | -$\sqrt{2}$ | D. | $\frac{1}{4}$ |
 一次越野跑中,当小明跑了1600米时,小刚跑了1400米,小明、小刚在此后所跑的路程y(米)与时间t(秒)之间的函数关系如图所示,则这次越野跑的全程为2200米.
一次越野跑中,当小明跑了1600米时,小刚跑了1400米,小明、小刚在此后所跑的路程y(米)与时间t(秒)之间的函数关系如图所示,则这次越野跑的全程为2200米.
 如图,梯形ABCD中,AD∥BC,∠B+∠C=90°,若AB=8,CD=5,试求BC-AD的值.
如图,梯形ABCD中,AD∥BC,∠B+∠C=90°,若AB=8,CD=5,试求BC-AD的值.