题目内容
13. 如图,O为△ABC的外心,△OCP为正三角形,OP与AC相交于D点,连接OA.若∠BAC=69°14′,AB=AC,则∠ADP的度数85°23′.
如图,O为△ABC的外心,△OCP为正三角形,OP与AC相交于D点,连接OA.若∠BAC=69°14′,AB=AC,则∠ADP的度数85°23′.
分析 利用三角形外心的性质以及利用等腰三角形的性质得出∠OAC=∠OCA=34°37′,进而结合三角形外角的性质得出答案.
解答 解:∵O为△ABC的外心,∠BAC=69°14′,AB=AC,
∴∠OAC=34°37′,AO=CO,
∴∠OAC=∠OCA=34°37′,
∴∠AOC=110°46′,
∵△OCP为正三角形,
∴∠AOP=50°46′,
∴∠ADP=∠OAD+∠AOD=85°23′.
故答案为:85°23′.
点评 此题主要考查了三角形的外心的性质以及等边三角形的性质等知识,得出∠OAC=∠OCA=34°37′是解题关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
4.根据下面的两种移动电话计费方式表,考虑下列问题.
(1)一个月本地通话时间200分钟和400分钟,计算按两种移动电话计费方式各需要交费多少元?
(2)会出现两种移动电话计费方式收费一样吗?如果会,请计算出此时的通话时间?如果不会,请说明理由;
(3)请你说明在怎样选择计费方式下更省钱?
| 方式一 | 方式二 | |
| 月租费 | 20元/月 | 50元/月 |
| 本地通话费 | 0.3元/分钟 | 0.2元/分钟 |
(2)会出现两种移动电话计费方式收费一样吗?如果会,请计算出此时的通话时间?如果不会,请说明理由;
(3)请你说明在怎样选择计费方式下更省钱?
1.如图,古希腊人常用小石子在沙滩上摆成各种形状来研究数.例如:称图中的数1,5,12,22…为五边形数,则第7个五边形数是( )
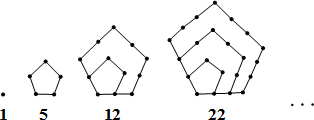

| A. | 62 | B. | 70 | C. | 84 | D. | 108 |
2.-4.5×10-5表示( )
| A. | -000045 | B. | -0.000045 | C. | -450000 | D. | -45000 |
3.2015年,永州市政府工作报告指出,要大力发展现代农业,做强优势产业,确保粮食面积825万亩,水果150万亩,蔬菜230万亩,烤烟25万亩.其中粮食面积825万亩中的“825万”用科学记数法表示为( )
| A. | 8.25×107 | B. | 8.25×106 | C. | 82.5×105 | D. | 0.825×107 |