题目内容
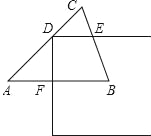
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 边上一点,且AD=3cm,动点
边上一点,且AD=3cm,动点![]() 从点
从点![]() 出发沿线段
出发沿线段![]() 向终点
向终点![]() 运动.作
运动.作![]() ,与边
,与边![]() 相交于点
相交于点![]() .
.
![]() 找出图中的一对相似三角形,并说明理由;
找出图中的一对相似三角形,并说明理由;
![]() 当
当![]() 为等腰三角形时,求
为等腰三角形时,求![]() 的长;
的长;
![]() 求动点
求动点![]() 从点
从点![]() 出发沿线段
出发沿线段![]() 向终点
向终点![]() 运动的过程中点
运动的过程中点![]() 的运动路线长.
的运动路线长.
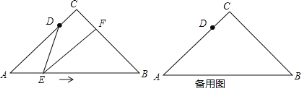
【答案】(1)![]() ;(2)
;(2)![]() 的长为
的长为![]() 或
或![]() 或
或![]() ;(3)
;(3)![]() cm.
cm.
【解析】
(1)由等腰直角三角形的性质得出∠A=∠B=45°由三角形的外角性质和已知条件证出∠ADE=∠BEF,即可得出结论;
(2)分三种情况:①若EF=BF,由相似三角形的性质和勾股定理求出AE=DE=![]() 即可;
即可;
②若EF=BE,由相似三角形的性质和勾股定理求出AE即可;
③若BF=BE,则∠FEB=∠EFB,由△ADE∽△BEF得出AE=AD=3即可.
(3)由(1)得出△ADE∽△BEF,得到![]() ,得出
,得出![]() 是
是![]() 的二次函数,即可得出结果.
的二次函数,即可得出结果.
解:![]() ,理由如下:
,理由如下:
∵在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
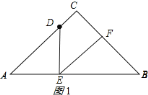
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ;
;
![]() 分三种情况
分三种情况
①如图![]() ,若
,若![]() ,则
,则![]() ,
,
又∵![]() ,
,
∴![]() ,
,
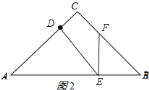
∴![]() ,
,
∴![]() ;
;
②如图![]() ,若
,若![]() ,则
,则![]()
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
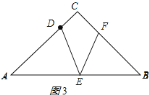
③如图![]() ,若
,若![]() ,则
,则![]()
又∵![]() ,
,
∴![]() ,
,
∴![]() .
.
综上所述,当![]() 为等腰三角形时,
为等腰三角形时,![]() 的长为
的长为![]() 或
或![]() 或
或![]() .
.
![]() 设
设![]() ,
,![]() 长为
长为![]() .
.
∵在![]() 中,
中,![]() ,
,![]() .
.
∴![]() ,
,![]() ,
,
由![]() 得:
得:![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴当![]() 时,
时,![]() 有最大值
有最大值![]() ,
,
∵从运动的过程中可以得出点![]() 运动的路程正好是
运动的路程正好是![]() ,
,
∴点![]() 运动路程为
运动路程为![]() .
.

练习册系列答案
相关题目