Question

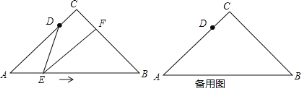
【题目】如图，在△ABG中，AB=AC=1，∠A=45°，边长为1的正方形的一个顶点D在边AG上，与△ADC另两边分别交于点E、F，DE∥AB，将正方形平移，使点D保持在AC上（D不与A重含），设AF=x，正方形与△ABC重叠部分的面积为y．

（1）求y与x的函数关系式并写出自变量x的取值范围；

（2）x为何值时y的值最大？

Answer 1

【答案】（1）（） （2）

【解析】

（1）当点D保持在AC上时，正方形与△ABC重叠部分为直角梯形DEBF，根据直角梯形的面积公式，只需用含x的代数式分别表示出上底DE、下底BF及高DF的长度即可．由△ADF为等腰直角三角形，可得高DF=AF=x；则AD=x，下底BF=AB-AF=1-x；进而得出CD=AC-AD=1-x，再根据等腰三角形及平行线的性质可证∠C=∠CED，得出上底DE=CD=1-x；根据点D保持在AC上，且D不与A重合，可知0＜AD≤1，从而求出自变量x的取值范围；
（2）由（1）知，y是x的二次函数，根据二次函数的性质，可知当x=-时，y的值最大；

解：（1）∵AB=AC，

∴∠B=∠C，

∵DE∥AB，

∴∠B=∠CED，∠AFD=∠FDE=90°，

∴∠C=∠CED，

∴DC=DE．

在Rt△ADF中，∵∠A=45°，

∴∠ADF=45°=∠A，

∴AF=DF=x，

∴AD=,

∴DC=DE=1﹣x，

∴y=（DE+FB）×DF=（1﹣x+1﹣x）x=﹣（+1）x2+x．

∵点D保持在AC上，且D不与A重合，

∴0＜AD≤1，

∴0＜x≤1，

∴0＜x≤．

故y=﹣（+1）x2+x，自变量x的取值范围是0＜x≤；

（2）∵y=﹣（+1）x2+x，

∴当x=-=﹣1时，y有最大值．