Question

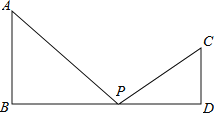
【题目】如图，AB⊥BD，CD⊥BD，AB=6cm，CD=4cm，BD=14cm，点p在BD上移动，当PB= ______ 时，△APB和△CPD相似．

Answer 1

【答案】8.4cm或12cm或2cm

【解析】

设出BP=xcm，由BD-BP=PD表示出PD的长，若△ABP∽△PDC，根据相似三角形的对应边成比例可得比例式，把各边的长代入即可列出关于x的方程，求出方程的解即可得到x的值，即为PB的长．

由AB=6cm，CD=4cm，BD=14cm，

设BP=xcm，则PD=（14-x）cm，

若△ABP∽△PDC，

则，

即，

变形得：14x-x2=24，即x2-14x+24=0，

因式分解得：（x-2）（x-12）=0，

解得：x1=2，x2=12，

所以BP=2cm或12cm时，△ABP∽△PDC；

若△ABP∽△CDP，

则，

即，

解得：x=8.4，

∴BP=8.4cm，

综上，BP=2cm或12cm或8.4cm时，△ABP∽△PDC．

故答案为：8.4cm或12cm或2cm．