题目内容
【题目】已知：如图，在
中，
度．
是
上一点，以为圆心、
为半径的圆与
交于点
，与
切于点
，
，
．设
是线段上的动点（与
、
不重合），
．
求
的长；
求
为何值时，以、、为顶点的三角形是等腰三角形；
在点的运动过程中，
与
的外接圆能否相切？若能，请证明；若不能，请说明理由；
请再提出一个与动点有关的数学问题，并直接写出答案．
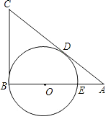
【答案】（1）BE= 3；（2）当x等于2、
、
时，△APD是等腰三角形；（3）PD与△PBC的外接圆不能相切，理由见解析；（4）答案不唯一，详见解析.
【解析】
（1）根据切线长定理即可解题；（2）根据不同的顶点分类讨论即可解题；（3）利用三边关系解题即可；（4）答案不唯一,见详解.
（1）∵AD与⊙O相切于点D，
∴AD2=AEAB；
由AD=2，AE=1，得AB=4；
∴BE=AB-AE=3；
（2）①以A为顶角顶点时，AP1=AD=2，x=BP1=BA-P1A=2；
②以P为顶角顶点时，作AD的垂直平分线P2F交AB于P2；
连接OD，则OD⊥AD，且OD∥P2F；
∴P2A=
OA=
x=BA-P2A=；
③以D为顶角顶点时，DP3=DA=2，过D作DM⊥AB于M，则DM∥BC；
由BC2+AB2=（AD+DC）2，得BC=DC=3，AM=
，AP3=2AM=
，
∴x=BA-P3A=2AM=，
综上所述，当x等于2、、时，△APD是等腰三角形；
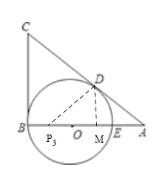
（3）PD与△PBC的外接圆不能相切；
理由：假设PD与△PBC的外接圆相切，
则PD⊥PC，
在Rt△PBC中，PC＞BC（直角三角形中，斜边大于直角边）
在Rt△PCD中，CD＞PC（直角三角形中，斜边大于直角边）
而BC=CD，与上面的矛盾，所以，不存在．
（4）答案不唯一，如：
①x为何值时，以P、D、A为顶点的三角形与△ABC相似；
答：当x=
或
时，以P、D、A为顶点的三角形与△ABC相似．
②当x为何值时，PD+PC的和最小；
答：当x=
时，PD+PC的和最小．
